题目内容
(本小题12分)
已知函数f(x)=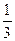 x
x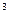 -(2a+1)
-(2a+1) x
x +3a(a+2)x+
+3a(a+2)x+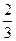 ,其中a为实数。
,其中a为实数。
(1)当a=-1时,求函数y=f(x)在[0,6]上的最大值与最小值;
(2)当函数y=f (x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
(x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
已知函数f(x)=
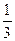 x
x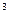 -(2a+1)
-(2a+1) x
x +3a(a+2)x+
+3a(a+2)x+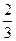 ,其中a为实数。
,其中a为实数。(1)当a=-1时,求函数y=f(x)在[0,6]上的最大值与最小值;
(2)当函数y=f
 (x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
(x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。(1)
 -1
-1(2)实数a的取值范围为-2<a≤0,或a=1,或2≤a<4
解: (1)当a=-1时,有f(x)=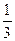 x
x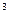 +x
+x ―3x+
―3x+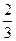 , f
, f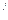 (x)= x
(x)= x +2x-3=0得x
+2x-3=0得x =1,x
=1,x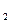 =-3,显然在区间[0,6]上只有根x
=-3,显然在区间[0,6]上只有根x =1; --------3分
=1; --------3分
由上表可知:y=f(x)在[0,6]上的最大值为 ,最小值为-1; --------6分
,最小值为-1; --------6分
(2)f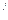 (x)=x
(x)=x -2(2a+1)x+3a(a+2)=[x-(a+2)](x―3a)=0得x
-2(2a+1)x+3a(a+2)=[x-(a+2)](x―3a)=0得x =a+2
=a+2 ,x
,x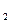 =3a
=3a
i、当a=1,即x =x
=x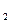 =3时,显然满足条件; ---------7分
=3时,显然满足条件; ---------7分
ii、当得x ≠x
≠x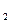 ,
,
若x >x
>x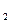 ,a+2>3a
,a+2>3a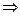 a<1,进而x
a<1,进而x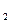 <x
<x <3, f
<3, f (x)在(0,6)上有唯一根,可知
(x)在(0,6)上有唯一根,可知
解得-2<a≤0
若x <x
<x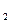
 a+2<3a
a+2<3a a>1,进而x
a>1,进而x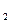 >x
>x >3, f
>3, f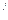 (x)在(0,6)有唯一根,知
(x)在(0,6)有唯一根,知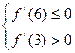
解得2≤a<4
所以实数a的取值范围为-2<a≤0,或a=1,或2≤a<4。 ---------12分
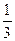 x
x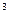 +x
+x ―3x+
―3x+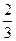 , f
, f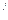 (x)= x
(x)= x +2x-3=0得x
+2x-3=0得x =1,x
=1,x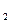 =-3,显然在区间[0,6]上只有根x
=-3,显然在区间[0,6]上只有根x =1; --------3分
=1; --------3分| x | 0 | (0,1) | 1 | (1,6) | 6 |
f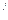 (x) (x) | | - | 0 | + | |
| f(x) | 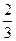 | ↘ | -1 | ↗ | 90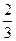 |
 ,最小值为-1; --------6分
,最小值为-1; --------6分(2)f
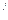 (x)=x
(x)=x -2(2a+1)x+3a(a+2)=[x-(a+2)](x―3a)=0得x
-2(2a+1)x+3a(a+2)=[x-(a+2)](x―3a)=0得x =a+2
=a+2 ,x
,x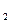 =3a
=3ai、当a=1,即x
 =x
=x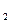 =3时,显然满足条件; ---------7分
=3时,显然满足条件; ---------7分ii、当得x
 ≠x
≠x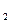 ,
,若x
 >x
>x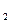 ,a+2>3a
,a+2>3a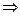 a<1,进而x
a<1,进而x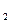 <x
<x <3, f
<3, f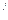 (x)在(0,6)上有唯一根,可知
(x)在(0,6)上有唯一根,可知
解得-2<a≤0
若x
 <x
<x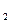
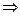 a+2<3a
a+2<3a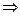 a>1,进而x
a>1,进而x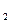 >x
>x >3, f
>3, f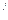 (x)在(0,6)有唯一根,知
(x)在(0,6)有唯一根,知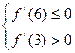
解得2≤a<4
所以实数a的取值范围为-2<a≤0,或a=1,或2≤a<4。 ---------12分

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
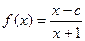 , 其中
, 其中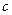 为常数,且函数
为常数,且函数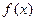 图像过原点.
图像过原点.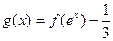 , 求函数
, 求函数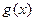 的零点
的零点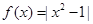 的单调递减区间为___________
的单调递减区间为___________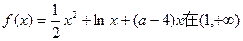 上是增函数.
上是增函数.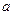 的取值范围;(6分)
的取值范围;(6分)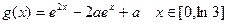 ,求函数
,求函数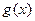 的最小值.(6分)
的最小值.(6分)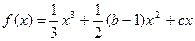 (b、c为常数).
(b、c为常数).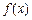 在
在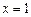 和
和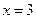 处取得极值,试求
处取得极值,试求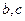 的值;
的值;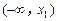 、
、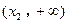 上单调递增,且在
上单调递增,且在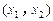 上单调递减,又满足
上单调递减,又满足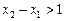 ,求证:
,求证: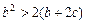 .
.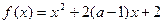 在区间(-∞,4]上是减函数,则实数a的取值范围是 ( )
在区间(-∞,4]上是减函数,则实数a的取值范围是 ( )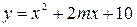 在区间
在区间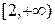 上是增函数,则实数
上是增函数,则实数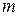 的取值范围
的取值范围 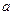 的取值范围
的取值范围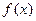 是定义在(-∞,+∞)上的奇函数,且
是定义在(-∞,+∞)上的奇函数,且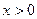 时,
时,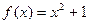 ,则
,则 时,
时,