题目内容
已知函数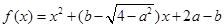 是偶函数,则函数图像与
是偶函数,则函数图像与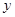 轴交点的纵坐标的最大值是( ).
轴交点的纵坐标的最大值是( ).
| A.- 4 | B.2 | C.3 | D.4 |
D
解析试题分析:由f(x)为偶函数可得b=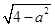 ,它表示以原点为圆心,以2为半径的上半圆;
,它表示以原点为圆心,以2为半径的上半圆;
f(x)图象与y轴交点的纵坐标是f(0)=2a-b,令t=2a-b,则b=2a-t,它表示斜率为2的直线.
如图: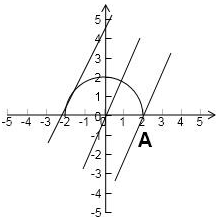
当直线过点A(2,0)时,在y轴上的截距-t最小,从而t最大,值为4
故选D.
考点:本题主要考查函数奇偶性的应用、数形结合求最值,有一定的综合性,能力要求较高
点评:解决该试题的关键是由f(x)为二次函数,故f(x)为偶函数时,对称轴为x=0,可求出a和b的关系.而f(x)图象与y轴交点的纵坐标是f(0)=2a-b,数形结合求最值即可.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
函数 的零点所在区间为
的零点所在区间为
A. | B. | C. | D. |
具有性质: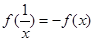 的函数,我们称为满足“倒负”变换的函数,下列函数:①
的函数,我们称为满足“倒负”变换的函数,下列函数:① ;②
;②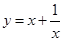 ;③
;③ 中满足“倒负”变换的函数是( )
中满足“倒负”变换的函数是( )
| A.①② | B.①③ | C.②③ | D.只有① |
函数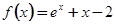 的零点所在的一个区间是( )
的零点所在的一个区间是( )
A. | B.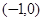 | C.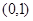 | D. |
下列函数中既是奇函数,又是增函数的是( )
A.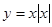 | B.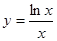 |
C.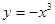 | D.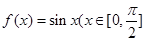 ) ) |
已知 是
是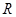 上最小正周期为
上最小正周期为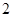 的周期函数,且当
的周期函数,且当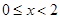 时,
时, ,则函数
,则函数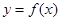 在区间
在区间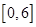 上的图像与
上的图像与 轴的交点个数为( )
轴的交点个数为( )
| A.6 | B.7 | C.8 | D.9 |
 时,函数
时,函数 和
和 的图象只可能是 ( )
的图象只可能是 ( )
 },B={y|1
},B={y|1 },下列图形表示集合A到集合B的函数图形的是( )
},下列图形表示集合A到集合B的函数图形的是( )