题目内容
当 时,函数
时,函数 和
和 的图象只可能是 ( )
的图象只可能是 ( )
B
解析试题分析:A中:y=ax+b当x=0时y=b>1,a>0,则y=bax为单调增函数但y=bax单调递减不满足条件,故A不正确;
B中:y=ax+b当x=0时0<y=b<1,a>0,可验证y=bax满足0<b<1,a>0,的条件,故B正确;
C中:y=ax+b当x=0时y=b>1,a<0,则y=bax为单调减函数,但是图中y=bax为单调减函数不满足条件,C不对;
D中、y=ax+b当x=0时0<y=b<1,a<0,则y=bax为单调增函数,但是图中y=bax为单调减函数不满足条件,D不对。故选B.
考点:指数函数的图像与性质;一次函数的图像与性质。
点评:本题主要考查指数函数的单调性与底数之间的关系,即当底数大于0小于1时函数单调递减,当底数大于1时函数单调递增。

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知 为定义在
为定义在 上的可导函数,且
上的可导函数,且 对于
对于 恒成立,则( )
恒成立,则( )
A. |
B. |
C. |
D. |
设 为实数,则
为实数,则 与
与 表示同一个函数的是 ( )
表示同一个函数的是 ( )
A. | B. |
C. | D. |
.函数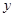 =
=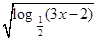 的定义域为( )
的定义域为( )
| A.[1,+∞) | B.[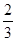 ,1] ,1] |
C.(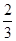 ,+∞) ,+∞) | D.(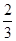 ,1] ,1] |
已知数列 满足:
满足: ,则
,则 =( )
=( )
A. | B. | C. | D. |
设α∈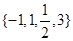 ,则使函数y=xα的定义域为R且为奇函数的所有α值为( )
,则使函数y=xα的定义域为R且为奇函数的所有α值为( )
| A.1,3 | B.-1,1 | C.-1,3 | D.-1,1,3 |
下列函数在定义域上是增函数的是( )
| A.f(x)=x2 | B.f(x)= |
| C.f(x)=tanx | D.f(x)=ln(1+ x) |
已知函数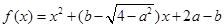 是偶函数,则函数图像与
是偶函数,则函数图像与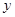 轴交点的纵坐标的最大值是( ).
轴交点的纵坐标的最大值是( ).
| A.- 4 | B.2 | C.3 | D.4 |
如果二次函数y=x2+mx+(m+3)有两个不同的零点,则m的取值范围是
| A.(-2,6) | B.[-2,6] |
| C.{-2,6} | D.(-∞,-2)∪(6,+∞) |