题目内容
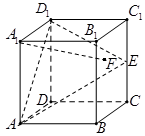
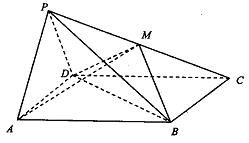
如图,在四棱锥P-ABCD中,侧面PAD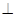 底面ABCD,侧棱
底面ABCD,侧棱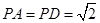 ,底面ABCD为直角梯形,其中BC//AD,AB
,底面ABCD为直角梯形,其中BC//AD,AB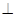 AD,AD=2,AB=BC=l,E为AD中点.
AD,AD=2,AB=BC=l,E为AD中点.
(1)求证:PE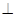 平面ABCD:
平面ABCD:
(2)求异面直线PB与CD所成角的余弦值:
(3)求平面PAB与平面PCD所成的二面角.

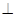 底面ABCD,侧棱
底面ABCD,侧棱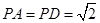 ,底面ABCD为直角梯形,其中BC//AD,AB
,底面ABCD为直角梯形,其中BC//AD,AB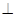 AD,AD=2,AB=BC=l,E为AD中点.
AD,AD=2,AB=BC=l,E为AD中点.(1)求证:PE
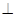 平面ABCD:
平面ABCD:(2)求异面直线PB与CD所成角的余弦值:
(3)求平面PAB与平面PCD所成的二面角.

(1)证明:在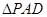 中,
中,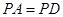 ,
,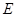 为
为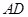 中点,
中点,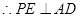 .又侧面
.又侧面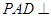 底面
底面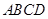 ,平面
,平面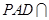 平面
平面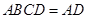 ,
,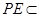 平面
平面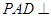 .
.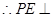 平面
平面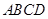 ;(2)
;(2)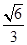 ;(3)
;(3)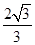 .
.
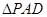 中,
中,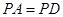 ,
,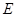 为
为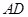 中点,
中点,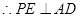 .又侧面
.又侧面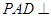 底面
底面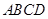 ,平面
,平面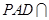 平面
平面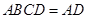 ,
,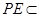 平面
平面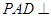 .
.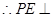 平面
平面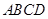 ;(2)
;(2)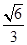 ;(3)
;(3)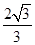 .
.试题分析:(1)由题意可根据面面垂直的性质定理来证,已知侧面
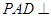 底面
底面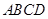 ,并且相交于
,并且相交于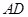 ,而
,而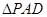 为等腰直角三角形,
为等腰直角三角形,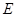 为
为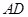 中点,所以
中点,所以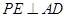 ,即
,即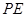 垂直于两个垂直平面的交线,且
垂直于两个垂直平面的交线,且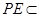 平面
平面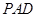 ,所以
,所以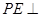 平面
平面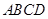 ;(2)连结
;(2)连结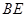 ,由题意可知
,由题意可知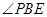 是异面直线
是异面直线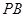 与
与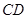 所成的角,并且三角形
所成的角,并且三角形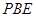 是直角三角形,
是直角三角形,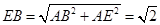 ,
,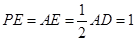 ,
,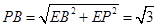 ,由余弦定理得
,由余弦定理得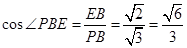 ;(3)利用体积相等法可得解,设点
;(3)利用体积相等法可得解,设点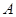 到平面
到平面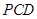 的距离
的距离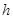 ,即由
,即由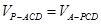 ,得
,得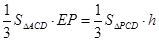 , 而在
, 而在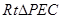 中,
中,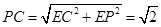 ,所以
,所以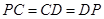 ,因此
,因此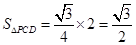 ,又
,又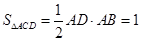 ,
,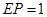 ,从而可得解.
,从而可得解.(1)证明:在
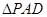 中,
中,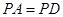 ,
,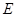 为
为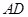 中点,
中点,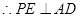 . 2分
. 2分又侧面
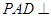 底面
底面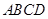 ,平面
,平面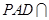 平面
平面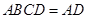 ,
,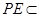 平面
平面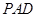 .
.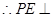 平面
平面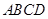 . 4分
. 4分(2)解:连结
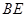 ,在直角梯形
,在直角梯形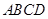 中,
中,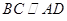 ,
,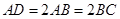 ,有
,有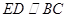 且
且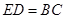 .所以四边形
.所以四边形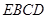 平行四边形,
平行四边形, .由(1)知
.由(1)知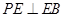 ,
,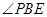 为锐角,所以
为锐角,所以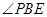 是异面直线
是异面直线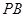 与
与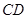 所成的角. 7分
所成的角. 7分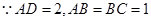 ,在
,在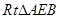 中,
中,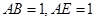 .
.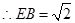 .在
.在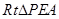 中,
中,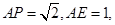
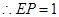 .在
.在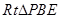 中,
中,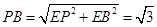 .
.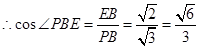 .
.所以异面直线
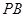 与
与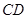 所成的角的余弦值为
所成的角的余弦值为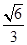 . 9分
. 9分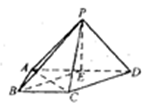
(3)解:由(2)得
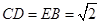 .在
.在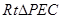 中,
中,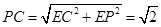 ,
,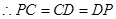 ,
, 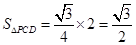 .
.设点
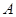 到平面
到平面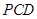 的距离
的距离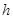 ,由
,由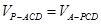 ,得
,得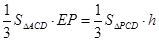 . 11分
. 11分又
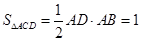 ,解得
,解得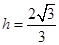 . 13分
. 13分
练习册系列答案
相关题目
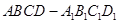 底面
底面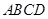 直角梯形,
直角梯形,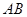 ∥
∥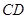 ,
,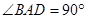 ,
,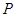 是棱
是棱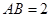 ,
,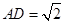 ,
,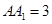 ,
,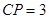 ,
,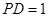 .
.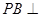 平面
平面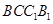 .
.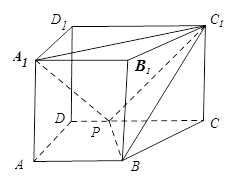
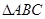 在平面
在平面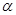 内,
内,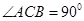 ,AB=2BC=2,P为平面
,AB=2BC=2,P为平面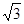 ,
,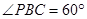
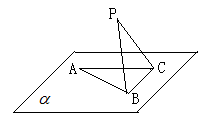
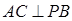
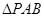 的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
的面积取得最大值时,求直线PC与平面PAB所成角的正弦值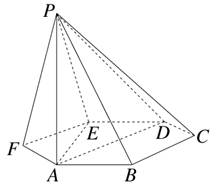
 表示平面,下列说法正确的是( )
表示平面,下列说法正确的是( )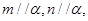 则
则
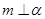 ,
,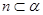 ,则
,则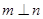
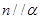
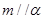 ,
,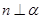
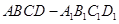 中,
中,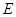 是棱
是棱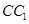 的中点,
的中点,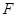 是侧面
是侧面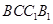 内的动点,且
内的动点,且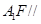 平面
平面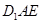 ,则
,则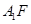 与平面
与平面