题目内容
已知函数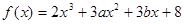 在
在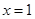 及
及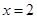 处取得极值.
处取得极值.
(1)求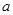 、
、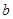 的值;(2)求
的值;(2)求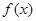 的单调区间.
的单调区间.
(1)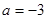 ,
,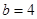 ;(2)
;(2)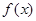 的单调增区间为
的单调增区间为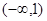 和
和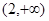 ,
,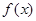 的单调减区间为
的单调减区间为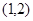 .
.
解析试题分析:(1)对函数求导可得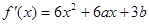 ,函数在
,函数在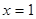 及
及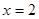 处取得极值,那么
处取得极值,那么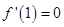 ,
,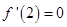 ,解关于
,解关于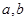 的方程组可得到
的方程组可得到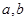 的值;(2)由(1)可得函数表达式为
的值;(2)由(1)可得函数表达式为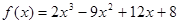 ,解
,解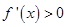 可得函数递增区间,解
可得函数递增区间,解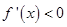 可得函数递减速区间.
可得函数递减速区间.
解:(1)由已知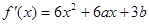
因为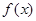 在
在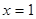 及
及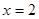 处取得极值,
处取得极值,
所以1和2是方程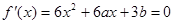 的两根
的两根
故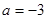 、
、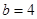
(2)由(1)可得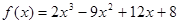
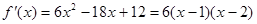
当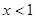 或
或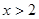 时,
时,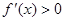 ,
,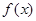 是增加的;
是增加的;
当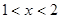 时,
时,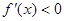 ,
,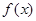 是减少的。
是减少的。
所以,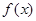 的单调增区间为
的单调增区间为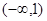 和
和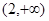 ,
,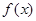 的单调减区间为
的单调减区间为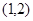
考点:1.函数的单调性与导数的关系;2.函数的极值.

练习册系列答案
相关题目
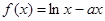 ,
,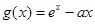 ,其中
,其中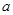 为实数,若
为实数,若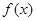 在
在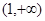 上是单调减函数,且
上是单调减函数,且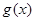 在
在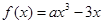 .
.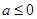 时,求函数
时,求函数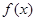 单调区间;
单调区间; ,求
,求 的值.
的值.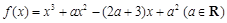 .
.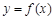 在
在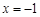 处的切线与直线
处的切线与直线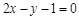 平行,求a的值;
平行,求a的值;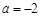 时,求
时,求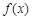 的单调区间.
的单调区间. x2-bx(b为常数).
x2-bx(b为常数). .
.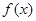 在
在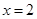 时取得极值,求实数
时取得极值,求实数 的值;
的值;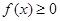 对任意
对任意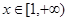 恒成立,求实数
恒成立,求实数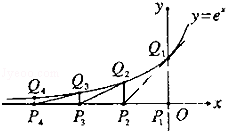
 .
. ,求曲线
,求曲线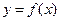 在点
在点 处的切线方程;
处的切线方程; 求函数
求函数 的单调区间;
的单调区间; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. +alnx(x>0).
+alnx(x>0). [f(x1)+f(x2)]≥f
[f(x1)+f(x2)]≥f 成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.