Question

（2010•山东模拟）在空间中，a、b、c是两两不重合的三条直线，α、β、γ是两两不重合的三个平面，下列命题正确的是（　　）

A．若两直线a、b分别与平面α平行，则a∥b

B．若直线a与平面β内的一条直线b平行，则a∥β

C．若直线a与平面β内的两条直线b、c都垂直，则a⊥β

D．若平面β内的一条直线a垂直平面γ，则γ⊥β

Answer 1

分析：对于A，可以翻译为：平行于同一个平面的两条直线平行，借助于几何模型--正方体，显然容易判别；对于B，考虑线面平行的判定及线面关系即可；对于C，由线面垂直的定义即可解决；对于D，可以由空间两平面垂直的判定解决．

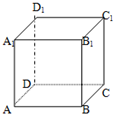
解答：解：A中，如图，A₁B₁∥面ABCD，B₁C₁∥面ABCD，但A₁B₁与B₁C₁相交，故不正确；
B中，如图，AD∥BC，BC?面ABCD，但是AD与面ABCD不平行，故不正确；
C中，如图，A₁A⊥AB，A₁A⊥A₁B₁，但A₁A与面A₁ABB₁不垂直，故不正确；
D中，若平面β内的一条直线a垂直平面γ，根据面面垂直的判定定理，则γ⊥β，正确．
故选D．

点评：本题考查线线关系、线面关系中的平行的判定、面面关系中垂直的判定，要注意判定定理与性质定理的综合运用．