题目内容
(本小题满分8分)已知数列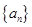 是首项为1,公比为2的等比数列,数列
是首项为1,公比为2的等比数列,数列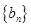 的前
的前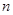 项和
项和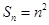 .
.
(1)求数列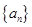 与
与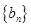 的通项公式;(2)求数列
的通项公式;(2)求数列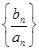 的前
的前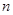 项和.
项和.
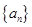 是首项为1,公比为2的等比数列,数列
是首项为1,公比为2的等比数列,数列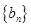 的前
的前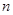 项和
项和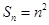 .
.(1)求数列
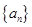 与
与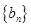 的通项公式;(2)求数列
的通项公式;(2)求数列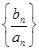 的前
的前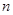 项和.
项和.(1)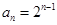 ,
,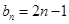 .(2)
.(2)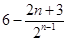 .
.
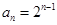 ,
,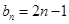 .(2)
.(2)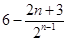 .
.本小题主要考查等差数列、等比数列等基础知识,考查运算求解能力和推理论证能力,求数列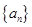 与
与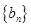 的通项公式时分别用到等比数列的通项公式及
的通项公式时分别用到等比数列的通项公式及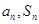 的关系;数列
的关系;数列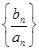 是差比数列,求和时用错位相减法,分别列出
是差比数列,求和时用错位相减法,分别列出  ,
,
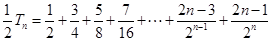 ,
,
解:(1)因为数列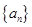 是首项为1,公比为2的等比数列,
是首项为1,公比为2的等比数列,
所以数列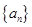 的通项公式为
的通项公式为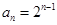 .
.
因为数列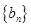 的前
的前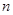 项和
项和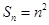 .
.
所以当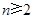 时,
时,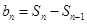
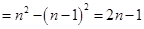 ,
,
当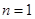 时,
时,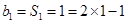 ,
,
所以数列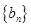 的通项公式为
的通项公式为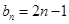 .
.
(2)由(1)可知,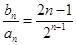 .
.
设数列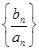 的前
的前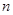 项和为
项和为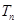 ,
,
则 , ①
, ①
即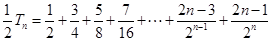 , ②
, ②
①-②,得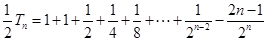
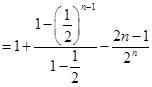
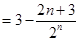 ,
,
所以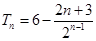 .
.
故数列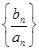 的前
的前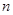 项和为
项和为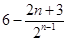 .
.
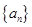 与
与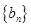 的通项公式时分别用到等比数列的通项公式及
的通项公式时分别用到等比数列的通项公式及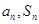 的关系;数列
的关系;数列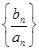 是差比数列,求和时用错位相减法,分别列出
是差比数列,求和时用错位相减法,分别列出  ,
, 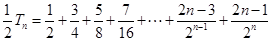 ,
,解:(1)因为数列
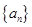 是首项为1,公比为2的等比数列,
是首项为1,公比为2的等比数列,所以数列
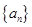 的通项公式为
的通项公式为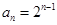 .
. 因为数列
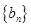 的前
的前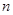 项和
项和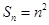 .
.所以当
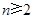 时,
时,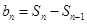
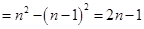 ,
,当
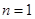 时,
时,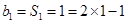 ,
,所以数列
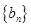 的通项公式为
的通项公式为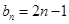 .
. (2)由(1)可知,
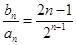 .
. 设数列
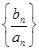 的前
的前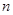 项和为
项和为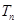 ,
,则
 , ①
, ①即
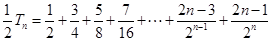 , ②
, ②①-②,得
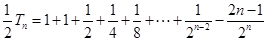
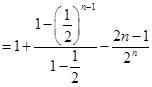
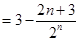 ,
, 所以
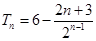 .
.故数列
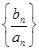 的前
的前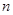 项和为
项和为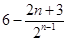 .
.
练习册系列答案
相关题目
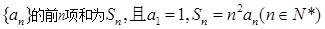 。
。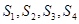 的值;
的值;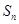 的表达式并用数学归纳法证明。
的表达式并用数学归纳法证明。 年比上一年增加
年比上一年增加 万吨,记2011年为第一年,甲、乙两工厂第
万吨,记2011年为第一年,甲、乙两工厂第 万吨和
万吨和 万吨.
万吨. ,
, 的通项公式;
的通项公式;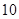 项的和为
项的和为 项的和为
项的和为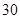 ,则前
,则前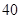 项的和为 ▲ .
项的和为 ▲ .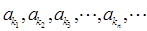 是等比数列,其中k1=1,k2=7,k3=25.
是等比数列,其中k1=1,k2=7,k3=25.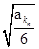 +
+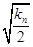 ,Sn=b12+b22+b32+…+ bn2, Tn=
,Sn=b12+b22+b32+…+ bn2, Tn= 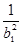 +
+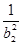 +
+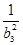 +…+
+…+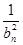 ,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。
,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。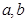 ,可按规则
,可按规则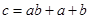 扩充为一个新数
扩充为一个新数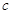 ,在
,在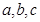 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.若
三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.若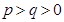 ,经过6次操作后扩充所得的数为
,经过6次操作后扩充所得的数为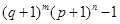 (
(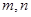 为正整数),则
为正整数),则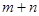 的值为 ▲ .
的值为 ▲ .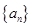 中,
中,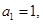 前
前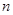 项和为
项和为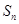 ,且点
,且点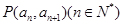 在直线
在直线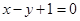 上,则
上,则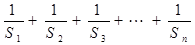 =( )
=( )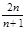

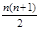
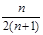
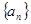 是各项正的等比数列,且
是各项正的等比数列,且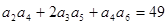 ,则
,则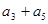 =
= 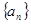 中,
中,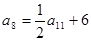 ,则数列
,则数列 项和
项和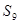 等于( )
等于( )


