题目内容
(本小题满分12分)有一牛奶商店每瓶牛奶进价为0.80元,售价为1元,但牛奶必须于每晚进货,于次日早晨出售;昨晚进货不多可能会因供不应求减少可得利润,若进货过多,次日早晨卖不完,则不能再隔夜出售(牛奶会发酸变质),每剩一瓶则造成0.80元的损失,过去的经验可以作为未来发展的参考,历史上200天的销售记录如下:
在统计的这200天当中,从未发生日销24瓶以下或29瓶以上的情况,我们可以假定日销24瓶以下或29瓶以上的情形不会发生,或者说此类事情发生的概率为零.作为经销商应如何确定每日进货数.
| 日销售量 | 天数 | 概率 |
| 25瓶 | 20 | 0.10 |
| 26瓶 | 60 | 0.30 |
| 27瓶 | 100 | 0.50 |
| 28瓶 | 20 | 0.10 |
见解析
分别计算购入25,26,27,28瓶是的条件利润和期望利润.注:条件利润:在购入一定量条件下能获得的利润 期望利润:条件利润乘以销售概率通过计算(略)可知:
购入25瓶时,期望利润为5.0元; 购入26瓶时,期望利润为5.1元; 购入27瓶时,期望利润为4.9元购入28瓶时,期望利润为4.2元. 由此可知,每晚购入26瓶可获得期望最大利润, 每晚购入26瓶牛奶的期望利润为5.10元仅为一个平均值,至于每天的实际情况不可预测.
购入25瓶时,期望利润为5.0元; 购入26瓶时,期望利润为5.1元; 购入27瓶时,期望利润为4.9元购入28瓶时,期望利润为4.2元. 由此可知,每晚购入26瓶可获得期望最大利润, 每晚购入26瓶牛奶的期望利润为5.10元仅为一个平均值,至于每天的实际情况不可预测.

练习册系列答案
相关题目
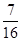
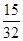
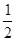
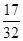
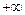 )
)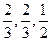 。这三项测试能否通过相互之间没有影响。
。这三项测试能否通过相互之间没有影响。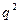
 列.
列.