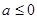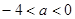题目内容
(本小题满分14分)
已知函数f(x)=(x2+ax-2a-3)·e3-x (a∈R)
(1)讨论f(x)的单调性;
(2)设g(x)=(a2+ )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
已知函数f(x)=(x2+ax-2a-3)·e3-x (a∈R)
(1)讨论f(x)的单调性;
(2)设g(x)=(a2+
 )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.⑴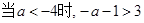 ,此时
,此时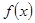 在
在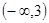 上为减函数,在
上为减函数,在 上为增函数,在
上为增函数,在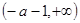 上为减函数;
上为减函数;
当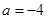 时,
时,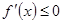 ,此时
,此时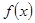 在
在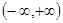 上为减函数;
上为减函数;
当 时,此时
时,此时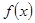 在
在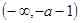 上为减函数,在
上为减函数,在 上为增函数,在
上为增函数,在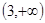 上为减函数.
上为减函数.
⑵ a的取值范围为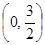 .
.
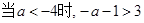 ,此时
,此时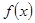 在
在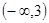 上为减函数,在
上为减函数,在 上为增函数,在
上为增函数,在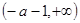 上为减函数;
上为减函数;当
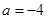 时,
时,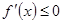 ,此时
,此时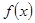 在
在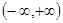 上为减函数;
上为减函数;当
 时,此时
时,此时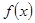 在
在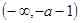 上为减函数,在
上为减函数,在 上为增函数,在
上为增函数,在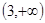 上为减函数.
上为减函数. ⑵ a的取值范围为
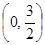 .
. 试题分析:⑴
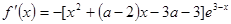 ,令
,令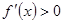 ,
,即
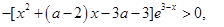 所以
所以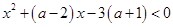
所以
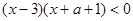 …………………………………………………………………3分
…………………………………………………………………3分 ,此时
,此时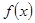 在
在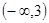 上为减函数,在
上为减函数,在 上为增函数,在
上为增函数,在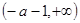 上为减函数;
上为减函数;当
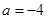 时,
时,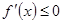 ,此时
,此时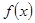 在
在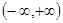 上为减函数;
上为减函数;当
 时,此时
时,此时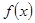 在
在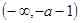 上为减函数,在
上为减函数,在 上为增函数,在
上为增函数,在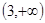 上为减函数. ………………………………………………………………………………6分
上为减函数. ………………………………………………………………………………6分⑵ 当
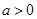 时,
时,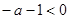 ,则
,则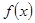 在
在 上为增函数,在
上为增函数,在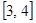 上为减函数
上为减函数又

∴
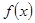 在
在 上的值域为
上的值域为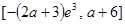 ………………………………………8分
………………………………………8分又
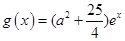 在
在 上为增函数,其值域为
上为增函数,其值域为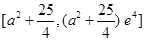 ……10分
……10分
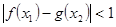 等价于
等价于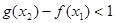 ……………………………………………12分
……………………………………………12分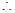 存在
存在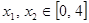 使得
使得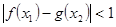 成立,只须
成立,只须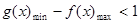
 ,又
,又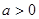
∴a的取值范围为
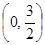 . ………………………………………………………………14分
. ………………………………………………………………14分点评:典型题,本题属于导数应用中的基本问题,(2)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,往往要利用“分离参数法”,本题最终化为最值之间故选的研究,体现考题“起点高,落点低”的特点。

练习册系列答案
相关题目
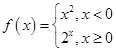 ,则
,则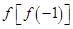 =
=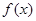 表示学生注意力随时间
表示学生注意力随时间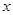 (分钟)的变化规律(
(分钟)的变化规律(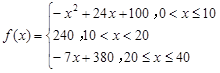
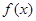 =
=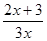 ,数列
,数列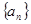 满足
满足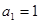 ,
,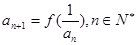 。(12分)
。(12分)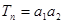 -
-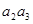 +
+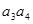 -
-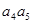 +…+
+…+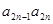 -
-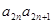 求
求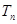 ;
;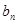 =
=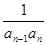 (
(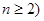 ,
,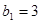 ,
,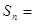
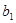 +
+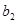 +
+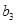 +┅
+┅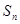 <
<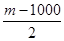 对一切
对一切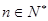 都成立,求最小的正整数
都成立,求最小的正整数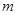 。
。
 (万元)和
(万元)和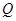 (万元),它们与投入资金
(万元),它们与投入资金 (万元)的关系有经验公式:
(万元)的关系有经验公式: 。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?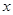 的方程
的方程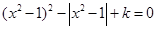 ,给出下列四个命题:
,给出下列四个命题: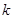 ,使得方程恰有2个不同实根; ②存在实数
,使得方程恰有2个不同实根; ②存在实数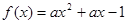 在
在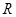 上恒满足
上恒满足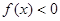 ,则
,则 的取值范围是
的取值范围是