题目内容
已知函数f(x)= sin ωx·cos ωx+cos 2ωx-
sin ωx·cos ωx+cos 2ωx- (ω>0),其最小正周期为
(ω>0),其最小正周期为 .
.
(1)求f(x)的解析式.
(2)将函数f(x)的图象向右平移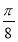 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围.
(1)sin (2)-
(2)- <k≤
<k≤ 或k=-1.
或k=-1.
【解析】(1)f(x)= sin ωx·cos ωx+cos 2ωx-
sin ωx·cos ωx+cos 2ωx- =
= sin 2ωx+
sin 2ωx+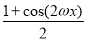 -
- =sin
=sin  ,由题意知f(x)的最小正周期T=
,由题意知f(x)的最小正周期T= ,T=
,T= =
= .
.
∴ω=2,∴f(x)=sin .
.
(2)将f(x)的图象向右平移 个单位后,得到
个单位后,得到
y=sin  的图象,再将所得图象所有点的横坐标伸长到原来的2倍(纵坐标不变),
的图象,再将所得图象所有点的横坐标伸长到原来的2倍(纵坐标不变),
得到y=sin  的图象.
的图象.
∴g(x)=sin  ,∵0≤x≤
,∵0≤x≤ ,
,
∴- ≤2x-
≤2x- ≤
≤ ,g(x)+k=0在区间
,g(x)+k=0在区间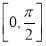 上有且只有一个实数解,即函数y=g(x)与y=-k在区间
上有且只有一个实数解,即函数y=g(x)与y=-k在区间 上有且只有一个交点,由正弦函数的图象可知-
上有且只有一个交点,由正弦函数的图象可知- ≤-k<
≤-k< 或-k=1.∴-
或-k=1.∴- <k≤
<k≤ 或k=-1.
或k=-1.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目