题目内容
13.设变量x,y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≥1}\\{y≥3x-3}\end{array}\right.$,则目标函数z=2x+y的取值范围是( )| A. | [$\frac{3}{2}$,2] | B. | [2,$\frac{9}{2}$] | C. | [$\frac{3}{2}$,3] | D. | [$\frac{3}{2}$,$\frac{9}{2}$] |
分析 根据已知的约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≥1}\\{y≥3x-3}\end{array}\right.$,画出满足约束条件的可行域,结合目标函数的几何意义求最大值、及最小值,进一步线出目标函数的值域.
解答 解:约约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≥1}\\{y≥3x-3}\end{array}\right.$,对应的平面区域如下图示:
由$\left\{\begin{array}{l}{y=x}\\{y=-x+1}\end{array}\right.$得到($\frac{1}{2}$,$\frac{1}{2}$),
由$\left\{\begin{array}{l}{y=x}\\{y=3x-3}\end{array}\right.$得到($\frac{3}{2}$,$\frac{3}{2}$),
由图易得目标函数z=2x+y在($\frac{1}{2}$,$\frac{1}{2}$)处取得最小值2×$\frac{1}{2}+\frac{1}{2}$=$\frac{3}{2}$,
在($\frac{3}{2}$,$\frac{3}{2}$)处取最大值2×$\frac{3}{2}$+$\frac{3}{2}$=$\frac{9}{2}$,
故z=2x+y的取值范围为:[$\frac{3}{2}$,$\frac{9}{2}$]
故选D.
点评 本题考查了线性规划问题,利用数形结合解答是关键.

练习册系列答案
相关题目
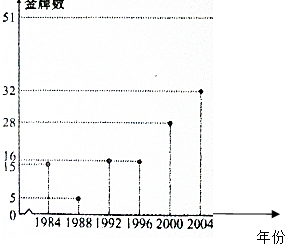 如图所示为1984年到2008年的奥运会中,我国每届奥运会获得的金牌数,设年份为x(x∈{1984,1988,1992,1996,2000,2004,2008}),金牌数为y,试判断y是否为x的函数,x是否为y的函数.
如图所示为1984年到2008年的奥运会中,我国每届奥运会获得的金牌数,设年份为x(x∈{1984,1988,1992,1996,2000,2004,2008}),金牌数为y,试判断y是否为x的函数,x是否为y的函数.