题目内容
6.函数f(x)=$\left\{\begin{array}{l}{2{x}^{2}-x-1,x≤0}\\{{3}^{x}-4,x>0}\end{array}\right.$的零点的个数为2.分析 分类讨论,函数对应方程根的个数,综合讨论结果,可得答案.
解答 解:当x≤0时,解2x2-x-1=0得:x=-$\frac{1}{2}$,或x=1(舍去),
当x>0时,解3x-4=0得:x=log34,
综上所述,函数f(x)=$\left\{\begin{array}{l}{2{x}^{2}-x-1,x≤0}\\{{3}^{x}-4,x>0}\end{array}\right.$有两个零点,
故答案为:2.
点评 本题考查的知识点是分段函数的应用,函数的零点,分类讨论思想,难度中档.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
17.如图所示的程序框图,运行后输出结果为( )
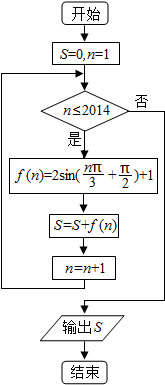

| A. | 2017 | B. | 4028 | C. | 2014 | D. | 2011 |
18.等差数列{an}中,a4=9,则前7项的和S7=( )
| A. | $\frac{63}{2}$ | B. | 28 | C. | 63 | D. | 36 |