题目内容
已知函数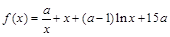 ,
,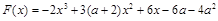 ,其中
,其中 且
且 .
.
(Ⅰ)当 ,求函数
,求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)若 时,函数
时,函数 有极值,求函数
有极值,求函数 图象的对称中心坐标;
图象的对称中心坐标;
(Ⅲ)设函数 (
( 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使 在
在 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
(Ⅰ) 单调增区间是
单调增区间是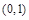 ,
,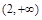 ;(II)
;(II)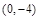 ;(III)
;(III)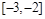
解析试题分析:(Ⅰ) 为确定函数的单调区间,往往遵循“求导数、求驻点、分区间讨论导数的正负、确定函数的单调性”等步骤.
(Ⅱ)为确定函数的极值,往往遵循“求导数、求驻点、分区间讨论导数的正负、确定函数的极值”等步骤.
本小题根据函数有极值,建立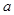 的方程,求得
的方程,求得 ,从而得到
,从而得到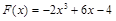 .根据
.根据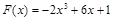 的图象可由
的图象可由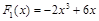 的图象向下平移4个单位长度得到,而
的图象向下平移4个单位长度得到,而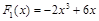 的图象关于
的图象关于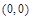 对称,
对称,
得到函数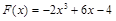 的图象的对称中心坐标.
的图象的对称中心坐标.
(Ⅲ)假设存在a使 在
在 上为减函数,通过讨论导函数为负数,得到
上为减函数,通过讨论导函数为负数,得到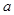 的不等式,达到解题目的.
的不等式,达到解题目的.
试题解析: (Ⅰ) (Ⅰ) 当 ,
,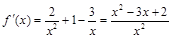 , 1分
, 1分
设 ,即
,即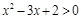 ,
,
所以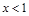 ,或
,或 , 2分
, 2分 单调增区间是
单调增区间是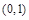 ,
,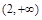 ; 4分
; 4分
(Ⅱ)当 时,函数
时,函数 有极值,
有极值,
所以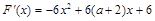 , 5分
, 5分
且 ,即
,即 , 6分
, 6分
所以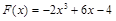 ,
,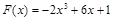 的图象可由
的图象可由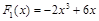 的图象向下平移4个单位长度得到,而
的图象向下平移4个单位长度得到,而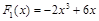 的图象关于
的图象关于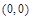 对称, 7分
对称, 7分
所以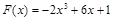 的图象的对称中心坐标为
的图象的对称中心坐标为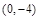 ; 8分
; 8分
(Ⅲ)假设存在a使 在
在 上为减函数,
上为减函数,
设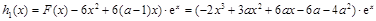 ,
,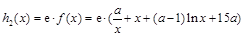 ,
,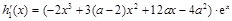 , 9分
, 9分
设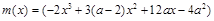 ,
,
当 在
在 上为减函数,则
上为减函数,则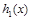 在
在 上为减函数,
上为减函数, 在
在 上为减函数,且
上为减函数,且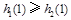 . 10分
. 10分
由(Ⅰ)知当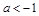 时,
时, 的单调减区间是
的单调减区间是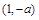 ,
,
由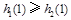 得:
得: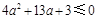 ,
,
解得: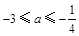 , 11分
, 11分
当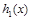 在
在 上为减函数时,对于
上为减函数时,对于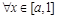 ,
,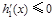 即
即 恒成立,
恒成立,
因为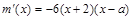 ,
,
(1)当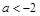 时,
时, 在
在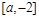 上是增函数,在
上是增函数,在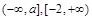 是减函数,
是减函数,
所以 在
在 上最大值为
上最大值为 ,
,
故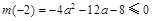 ,
,
即 ,或
,或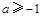 ,故
,故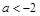 ; 12分
; 12分
(2)当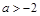 时,
时, 在
在 上是增函数,在
上是增函数,在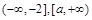 是减函数,
是减函数,
所以 在
在

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
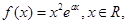 其中
其中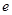 为自然对数的底数,
为自然对数的底数, 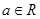 .
.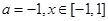 ,求函数
,求函数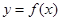 的最值;
的最值;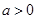 ,都有
,都有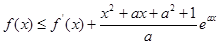 成立,求
成立,求 的取值范围.
的取值范围.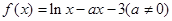
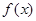 的单调性;
的单调性;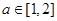 ,若函数
,若函数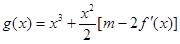 在 区间
在 区间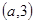 上有最值,求实数
上有最值,求实数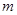 的取值范围.
的取值范围. 。
。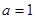 ,求函数
,求函数 的单调递减区间;
的单调递减区间;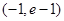 上单调递增,求实数
上单调递增,求实数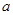 的取值范围;
的取值范围;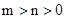 时,
时,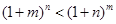
 =
= ,
, =
= ,若曲线
,若曲线 和曲线
和曲线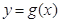 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线 .
. ,
, ,
, ,
, 的值;
的值; 时,
时, ≤
≤ ,求
,求 的取值范围.
的取值范围.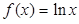 .
.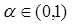 ,求
,求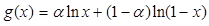 最大值;
最大值;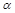 ,
,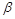 满足
满足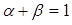 .求证:
.求证: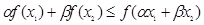 ;
;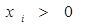 ,正数
,正数 满足
满足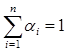 .证明:
.证明: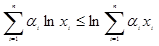
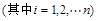 .
. +
+ ,g(x)=
,g(x)= ln(2ex)(其中e为自然对数的底数)
ln(2ex)(其中e为自然对数的底数) }中,a1=1,
}中,a1=1,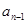 )(n≥2),求证:
)(n≥2),求证: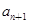 <
< <
< .
. 和
和 是函数
是函数 的两个极值点,其中
的两个极值点,其中 ,
, .
. 的取值范围;
的取值范围; ,求
,求 的最大值.注:e是自然对数的底.
的最大值.注:e是自然对数的底. 的图像过原点,
的图像过原点, ,
, 的导函数为
的导函数为 ,且
,且 ,
,

 ,
, 的解析式;
的解析式; 的极小值;
的极小值; 和
和 ,使得
,使得 和
和 若存在,求出
若存在,求出