题目内容
(本题满分15分)设椭圆 :
: ,直线
,直线 过椭圆左焦点
过椭圆左焦点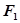 且不与
且不与 轴重合,
轴重合, 与椭圆交于
与椭圆交于 ,当
,当 与
与 轴垂直时,
轴垂直时, ,
, 为椭圆的右焦点,
为椭圆的右焦点,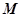 为椭圆
为椭圆 上任意一点,若
上任意一点,若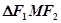 面积的最大值为
面积的最大值为 。
。
(1)求椭圆 的方程;
的方程;
(2)直线 绕着
绕着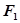 旋转,与圆
旋转,与圆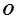 :
: 交于
交于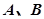 两点,若
两点,若 ,求
,求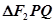 的面积
的面积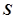 的取值范围。
的取值范围。
【答案】
(1)设椭圆半焦距为 ①,将
①,将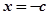 代入椭圆方程得
代入椭圆方程得 ,∴
,∴
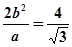 ②;又由已知得
②;又由已知得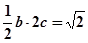 ③;由①②③解得
③;由①②③解得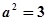 、
、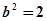 、
、
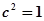 。所求椭圆方程为:
。所求椭圆方程为: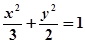 。
。
(2)设直线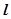 :
: 即
即 ,圆心
,圆心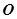 到
到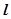 的距离
的距离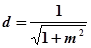 ,由圆性质:
,由圆性质: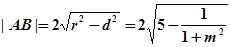 ,又
,又 ,得
,得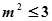 。
。
联立方程组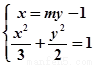 ,消去
,消去 得
得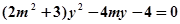 。
。
设 ,则
,则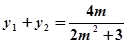 ,
,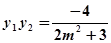 。
。
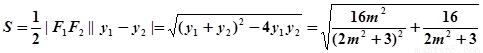
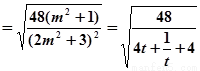 (令
(令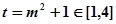 )。
)。
设 ,
,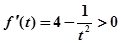 对
对 恒成立,
恒成立,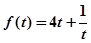 在
在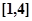 上为增函数,
上为增函数,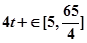 ,所以,
,所以,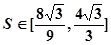 。
。
【解析】略

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
 .
. 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值; 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 为自然对数的底数.
为自然对数的底数.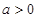 ,函数
,函数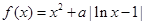 .
. 时,求函数
时,求函数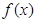 的单调增区间;
的单调增区间; 时,不等式
时,不等式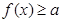 恒成立,实数
恒成立,实数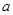 的取值范围.
的取值范围.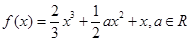 .
.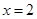 时,
时,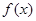 取得极值,求
取得极值,求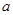 的值;
的值;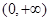 内为增函数,求
内为增函数,求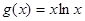 ,是否存在正实数
,是否存在正实数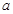 ,使得对任意
,使得对任意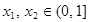 ,都有
,都有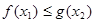 成立?
成立?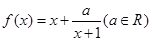 .
.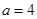 时,解不等式:
时,解不等式: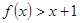 ;
;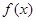 在
在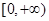 的最小值;
的最小值;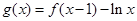 的单调递增区间.
的单调递增区间.