题目内容
已知非零向量
和
满足
⊥(
-
),
⊥(2
-
),则
与
的夹角为( )
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
分析:先根据
⊥(
-
),
⊥(2
-
)则数量积为0,可求出|
|与|
|的关系,再根据数量积公式可求出
与
的夹角.
| a |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答:解:∵
⊥(
-
),
⊥(2
-
),
∴
•(
-
)=0,
•(2
-
)=0,
即
2-
•
=0且2
•
-
2=0,
∴消去
•
得|
|=
|
|,
设
与
的夹角为θ,
则
2-
•
=|
|2-|
|×
|
|cosθ=0,
∵非零向量
,
∴cosθ=
,
∵θ∈[0,π]
∴θ=
.
故选A.
| a |
| a |
| b |
| b |
| a |
| b |
∴
| a |
| a |
| b |
| b |
| a |
| b |
即
| a |
| a |
| b |
| a |
| b |
| b |
∴消去
| a |
| b |
| b |
| 2 |
| a |
设
| a |
| b |
则
| a |
| a |
| b |
| a |
| a |
| 2 |
| a |
∵非零向量
| a |
∴cosθ=
| ||
| 2 |
∵θ∈[0,π]
∴θ=
| π |
| 4 |
故选A.
点评:本题主要考查了向量垂直的充要条件及向量的数量积公式,同时考查了运算求解的能力和消元的思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, 和
和 满足(
满足(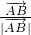 +
+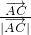 )•
)•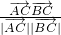 =
= ,则三角形ABC是
,则三角形ABC是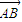 ,
,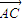 和
和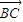 满足(
满足(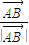 +
+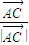 )•
)•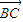 =0,且
=0,且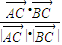 =
=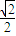 ,则三角形ABC是( )
,则三角形ABC是( )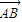 ,
,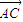 和
和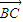 满足(
满足(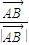 +
+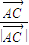 )•
)•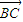 =0,且
=0,且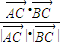 =
=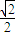 ,则三角形ABC是( )
,则三角形ABC是( )