题目内容
已知非零向量 ,
, 和
和 满足(
满足(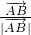 +
+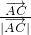 )•
)• =0,且
=0,且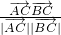 =
= ,则三角形ABC是
,则三角形ABC是
- A.等边三角形
- B.等腰非直角三角形
- C.非等腰三角形
- D.等腰直角三角形
D
分析:由非零向量 ,
, 和
和 满足(
满足(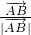 +
+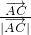 )•
)• =0,知∠A的角平分线与BC边垂直,由
=0,知∠A的角平分线与BC边垂直,由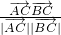 =
= ,知cos∠C=
,知cos∠C= ,由此能导出△ABC为等腰直角三角形.
,由此能导出△ABC为等腰直角三角形.
解答:∵非零向量 ,
, 和
和 满足(
满足(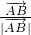 +
+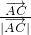 )•
)• =0,
=0,
∴∠A的角平分线与BC边垂直,
∴△ABC为等腰三角形,
∵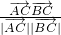 =
= ,
,
∴cos∠C=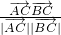 =
= ,
,
∴∠C为45度,
故△ABC为等腰直角三角形.
故选D.
点评:本题考查向量在几何中的应用,是中档题.解题时要认真审题,仔细解答,注意平面向量数量积的合理运用.
分析:由非零向量
 ,
, 和
和 满足(
满足(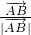 +
+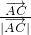 )•
)• =0,知∠A的角平分线与BC边垂直,由
=0,知∠A的角平分线与BC边垂直,由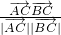 =
= ,知cos∠C=
,知cos∠C= ,由此能导出△ABC为等腰直角三角形.
,由此能导出△ABC为等腰直角三角形.解答:∵非零向量
 ,
, 和
和 满足(
满足(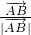 +
+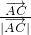 )•
)• =0,
=0,∴∠A的角平分线与BC边垂直,
∴△ABC为等腰三角形,
∵
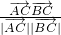 =
= ,
,∴cos∠C=
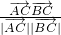 =
= ,
,∴∠C为45度,
故△ABC为等腰直角三角形.
故选D.
点评:本题考查向量在几何中的应用,是中档题.解题时要认真审题,仔细解答,注意平面向量数量积的合理运用.

练习册系列答案
相关题目
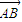 ,
,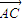 和
和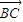 满足(
满足(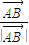 +
+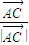 )•
)•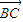 =0,且
=0,且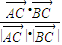 =
=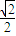 ,则三角形ABC是( )
,则三角形ABC是( )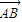 ,
,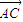 和
和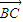 满足(
满足(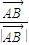 +
+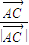 )•
)•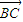 =0,且
=0,且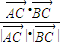 =
=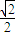 ,则三角形ABC是( )
,则三角形ABC是( )