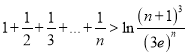题目内容
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 的定义域和值域;
的定义域和值域;
(Ⅱ)若函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(Ⅰ)定义域为![]() ,值域为
,值域为![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由![]() ,得到
,得到![]() ,由
,由![]() ,求解,即可得出定义域;令
,求解,即可得出定义域;令![]() ,得到
,得到![]() ,根据判别式法,即可求出结果;
,根据判别式法,即可求出结果;
(Ⅱ)由定义域为![]() 可得:
可得:![]() 恒成立,即
恒成立,即![]() ,令
,令![]() ,由于
,由于![]() 的值域为
的值域为![]() ,则
,则![]() ,又
,又![]() ,根据判别式大于等于0,解集为
,根据判别式大于等于0,解集为![]() ,得到
,得到![]() 和
和![]() 是方程
是方程![]() 的两个根,由根与系数关系,列出方程组,求解,即可得出结果.
的两个根,由根与系数关系,列出方程组,求解,即可得出结果.
(Ⅰ)若![]() ,则
,则![]() ,由
,由![]() ,得到
,得到
![]() ,得到
,得到![]() ,故定义域为
,故定义域为![]() .
.
令![]() ,则
,则![]()
当![]() 时,
时,![]() 符合.
符合.
当![]() 时,上述方程要有解,则
时,上述方程要有解,则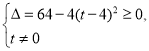 ,得到
,得到![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() ,则值域为
,则值域为![]() .
.
(Ⅱ)由于函数![]() 的定义域为
的定义域为![]() ,则
,则![]() 恒成立,则
恒成立,则![]() ,即
,即![]() ,令
,令![]() ,由于
,由于![]() 的值域为
的值域为![]() ,则
,则![]() ,而
,而
![]() ,则由
,则由![]() 解得
解得![]() ,故
,故![]() 和
和![]() 是方程
是方程![]() 即
即![]() 的两个根,则
的两个根,则![]() ,得到
,得到![]() ,符合题意.所以
,符合题意.所以![]() .
.

练习册系列答案
相关题目