题目内容
求下列各曲线的标准方程
(Ⅰ)实轴长为12,离心率为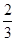 ,焦点在x轴上的椭圆;
,焦点在x轴上的椭圆;
(Ⅱ)抛物线的焦点是双曲线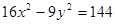 的左顶点.
的左顶点.
【答案】
(1) (2)
(2)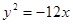
【解析】
试题分析:解:(Ⅰ)设椭圆的标准方程为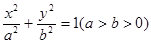 1分
1分
由已知,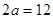 ,
,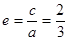 3分
3分
 5分
5分
所以椭圆的标准方程为 .
6分
.
6分
(Ⅱ)由已知,双曲线的标准方程为 ,其左顶点为
,其左顶点为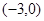 7分
7分
设抛物线的标准方程为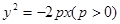 , 其焦点坐标为
, 其焦点坐标为 , 9分
, 9分
则 即
即 所以抛物线的标准方程为
所以抛物线的标准方程为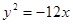 .
12分
.
12分
考点:本试题考查了圆锥曲线的方程的求解。
点评:对于椭圆的方程的求解主要是求解参数a,b的值,结合已知中的椭圆的性质得到其关系式,同时利用a,b,c的平方关系来得到结论,对于抛物线的求解,只有一个参数p,因此只要一个点的坐标即可,或者一个性质都可以解决,属于基础题。

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目