题目内容
设函数f(x)=ax![]() +bx+1(a,b为实数),F(x)=
+bx+1(a,b为实数),F(x)=![]()
(1)若f(-1)=0且对任意实数x均有f(x)![]() 成立,求F(x)表达式。
成立,求F(x)表达式。
(2)在(1)的条件下,当x![]() 时,g(x)=f(x)-kx是单调函数,求实数k的取值范围。
时,g(x)=f(x)-kx是单调函数,求实数k的取值范围。
(3)(理)设m>0,n<0且m+n>0,a>0且f(x)为偶函数,求证:F(m)+F(n)>0。
(1)F(x)=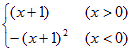 (2)k
(2)k![]() -2或k
-2或k![]() 6(3)见解析
6(3)见解析
解析:
(1)![]() f(-1)=0 ∴
f(-1)=0 ∴![]() 由f(x)
由f(x)![]() 0恒成立 知△=b
0恒成立 知△=b![]() -4a=(a+1)
-4a=(a+1)![]() -4a=(a-1)
-4a=(a-1)![]() 0
0
∴a=1从而f(x)=x![]() +2x+1 ∴F(x)=
+2x+1 ∴F(x)=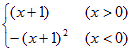 ,
,
(2)由(1)可知f(x)=x![]() +2x+1 ∴g(x)=f(x)-kx=x
+2x+1 ∴g(x)=f(x)-kx=x![]() +(2-k)x+1,由于g(x)在
+(2-k)x+1,由于g(x)在![]() 上是单调函数,知-
上是单调函数,知-![]() 或-
或-![]() ,得k
,得k![]() -2或k
-2或k![]() 6 ,
6 ,
(3)![]() f(x)是偶函数,∴f(x)=f(x),而a>0∴
f(x)是偶函数,∴f(x)=f(x),而a>0∴![]() 在
在![]() 上为增函数
上为增函数
对于F(x),当x>0时-x<0,F(-x)=-f(-x)=-f(x)=-F(x),当x<0时-x>0,F(-x)=f(-x)=f(x)=-F(x),
∴F(x)是奇函数且F(x)在![]() 上为增函数,
上为增函数,
![]() m>0,n<0,由m>-n>0知F(m)>F(-n)∴F(m)>-F(n)
m>0,n<0,由m>-n>0知F(m)>F(-n)∴F(m)>-F(n)
∴F(m)+F(n)>0 。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目