题目内容
设函数f(x)=ax-
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0,
(1)求y=f(x)的解析式,并求其单调区间;
(2)用阴影标出曲线y=f(x)与此切线以及x轴所围成的图形,并求此图形的面积.
| b | x |
(1)求y=f(x)的解析式,并求其单调区间;
(2)用阴影标出曲线y=f(x)与此切线以及x轴所围成的图形,并求此图形的面积.
分析:(1)求导函数,利用切线方程,建立方程组,即可求y=f(x)的解析式,从而可得单调区间;
(2)作出函数图象,可得曲线y=f(x)与此切线以及x轴所围成的图形,利用定积分,可求面积.
(2)作出函数图象,可得曲线y=f(x)与此切线以及x轴所围成的图形,利用定积分,可求面积.
解答:解:(1)求导函数,可得f′(x)=a+
∵曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0,
∴f′(2)=
,f(2)=
∴
,∴a=1,b=3
∴f(x)=x-
,f′(x)=1+
∴函数的单调增区间为(-∞,0),(0,+∞);
(2)曲线y=f(x)与此切线以及x轴所围成的图形,如图所示
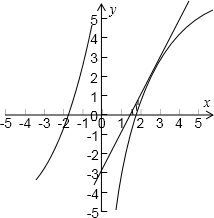
由7x-4y-12=0,可得y=
x-3,令y=0,可得x=
∴阴影部分的面积为
[(
x-3)-(x-
)]=(
x2-3x+3lnx)
=-
+3ln
.
| b |
| x2 |
∵曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0,
∴f′(2)=
| 7 |
| 4 |
| 1 |
| 2 |
∴
|
∴f(x)=x-
| 3 |
| x |
| 3 |
| x2 |
∴函数的单调增区间为(-∞,0),(0,+∞);
(2)曲线y=f(x)与此切线以及x轴所围成的图形,如图所示

由7x-4y-12=0,可得y=
| 7 |
| 4 |
| 12 |
| 7 |
∴阴影部分的面积为
| ∫ | 2
|
| 7 |
| 4 |
| 3 |
| x |
| 3 |
| 8 |
| | | 2
|
| 315 |
| 686 |
| 7 |
| 6 |
点评:本题考查导数知识的运用,考查导数的几何意义,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目