题目内容
本小题满分10分)选修4-1:几何证明选讲
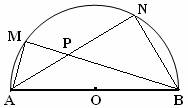 如图,在直径是AB的半圆上有两个不同的点M、N,设AN与BM的交点是P.求证:
如图,在直径是AB的半圆上有两个不同的点M、N,设AN与BM的交点是P.求证:![]() .
.
证明:过点P作PE⊥AB于E,
∵AB为直径,∴∠ANB=∠AMB=![]() ,
,
 ∴P,E,B,N四点共圆,P,E,A,M四点共圆.
∴P,E,B,N四点共圆,P,E,A,M四点共圆.
由割线定理得,AE·AB=AP·AN ① , BE·AB=BP·BM ②,
由①+②得,AB(AE+BE)=AP·AN+BP·BM,即AP·AN+BP·BM=![]() .
.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答, ,求证:
,求证: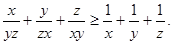
 ,求证:
,求证: