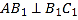题目内容
【题目】已知两点
，
，点
是圆
上任意一点，则
的面积最小值是（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
试题先由A和B的坐标，确定出直线AB的解析式，再把圆的方程化为标准方程，找出圆心坐标和半径，利用点到直线的距离公式求出圆心到直线AB的距离d，用d-r求出圆上到直线AB距离最小的点到直线AB的距离，即为所求的C点，三角形ABC边AB边上的高即为d-r，故利用两点间的距离公式求出线段AB的长度，利用三角形的面积公式即可求出此时三角形的面积，即为所求面积的最小值．
由于两点
,则根据两点的距离公式得到|AB|=
,而求解的三角形面积的最小值即为高的最小值，那么圆心（1，0）到直线AB：y-x=2的距离
，半径为1，故圆上点到直线AB距离的最小值为d-1,那么利用三角形的面积公式得到为
，故答案为
【题目】 某汽车租赁公司为了调查A, B两种车型的出租情况，现随机抽取这两种车型各50辆，分别统计了每辆车在某个星期内的出租天数，统计数据如下表:
A型车
出租天数 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 3 | 30 | 5 | 7 | 5 |
B型车
出租天数 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 10 | 10 | 15 | 10 | 5 |
(1)试根据上面的统计数据，判断这两种车型在本星期内出租天数的方差的大小关系(只需写出结果);
(2)现从出租天数为3天的汽车(仅限A, B两种车型)中随机抽取一辆，试估计这辆汽车是A型车的概率;
(3)如果两种车型每辆车每天出租获得的利润相同，该公司需要购买一辆汽车，请你根据所学的统计知识，给出建议应该购买哪一种车型，并说明你的理由．
【题目】随着人们经济收入的不断增长，个人购买家庭轿车已不再是一种时尚．车的使用费用，尤其是随着使用年限的增多，所支出的费用到底会增长多少，一直是购车一族非常关心的问题．某汽车销售公司做了一次抽样调查，并统计得出某款车的使用年限
（单位：年）与所支出的总费用
（单位：万元）有如下的数据资料：
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知对呈线性相关关系．
线性回归方程系数公式：
，
.
（1）试求线性回归方程
的回归系数
，
；
（2）当使用年限为10年时，估计车的使用总费用．
