��Ŀ����
ij��ֽ���⽨һ������ͼ��Ϊ���������Ϊ162ƽ����������ˮ�����أ��ص����һ��(ƽ��ͼ��ͼ��ʾ)�����������Χǽ���쵥��Ϊ400Ԫ/�ף��м�������ǽ���쵥��Ϊ248Ԫ/�ף��ص��쵥��Ϊ80Ԫ/ƽ���ף�ˮ������ǽ�ĺ�Ⱥ��Բ��ƣ�

(1)�������ˮ�����صij��Ϳ���ʹ�������ͣ�������������ۣ�
(2)�����ڵ������ƣ��óصij��Ϳ������ܳ���16�ף��������ˮ�����صij��Ϳ���ʹ�������ͣ�������������ۣ�

(1)�������ˮ�����صij��Ϳ���ʹ�������ͣ�������������ۣ�
(2)�����ڵ������ƣ��óصij��Ϳ������ܳ���16�ף��������ˮ�����صij��Ϳ���ʹ�������ͣ�������������ۣ�
��1������Ϊ16.2�ף���Ϊ10��ʱ�������ͣ���������Ϊ38 880Ԫ
��2������Ϊ16�ף���Ϊ10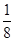 ��ʱ�������ͣ���������Ϊ38 882Ԫ��
��ʱ�������ͣ���������Ϊ38 882Ԫ��
��2������Ϊ16�ף���Ϊ10
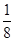 ��ʱ�������ͣ���������Ϊ38 882Ԫ��
��ʱ�������ͣ���������Ϊ38 882Ԫ��(1)����ˮ�����صĿ�Ϊx�ף���Ϊ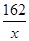 �ף�
�ף�
�������f(x)��400��(2x��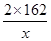 )��248��2x��80��162��1 296x��
)��248��2x��80��162��1 296x�� ��12 960
��12 960
��1 296(x��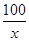 )��12 960
)��12 960
��1 296��2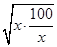 ��12 960��38 880(Ԫ)��
��12 960��38 880(Ԫ)��
���ҽ���x��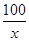 (x>0)����x��10ʱȡ�Ⱥţ�
(x>0)����x��10ʱȡ�Ⱥţ�
�൱��Ϊ16.2�ף���Ϊ10��ʱ�������ͣ���������Ϊ38 880Ԫ��
(2)����������֪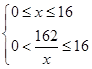 ����10
����10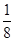 ��x��16��
��x��16��
��g(x)��x��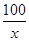 (10
(10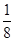 ��x��16)��
��x��16)��
g(x)��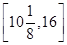 ������������
������������
�൱x��10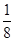 ʱ����ʱ
ʱ����ʱ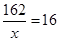 ����
����
g(x)����Сֵ����f(x)����Сֵ��
��Ϊ1 296��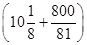 ��12 960��38 882Ԫ��
��12 960��38 882Ԫ��
�൱��Ϊ16�ף���Ϊ10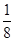 ��ʱ�������ͣ���������Ϊ38 882Ԫ��
��ʱ�������ͣ���������Ϊ38 882Ԫ��
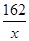 �ף�
�ף��������f(x)��400��(2x��
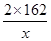 )��248��2x��80��162��1 296x��
)��248��2x��80��162��1 296x�� ��12 960
��12 960��1 296(x��
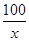 )��12 960
)��12 960��1 296��2
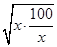 ��12 960��38 880(Ԫ)��
��12 960��38 880(Ԫ)�����ҽ���x��
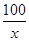 (x>0)����x��10ʱȡ�Ⱥţ�
(x>0)����x��10ʱȡ�Ⱥţ��൱��Ϊ16.2�ף���Ϊ10��ʱ�������ͣ���������Ϊ38 880Ԫ��
(2)����������֪
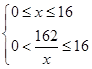 ����10
����10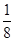 ��x��16��
��x��16����g(x)��x��
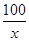 (10
(10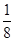 ��x��16)��
��x��16)��g(x)��
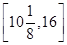 ������������
�������������൱x��10
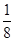 ʱ����ʱ
ʱ����ʱ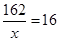 ����
����g(x)����Сֵ����f(x)����Сֵ��
��Ϊ1 296��
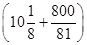 ��12 960��38 882Ԫ��
��12 960��38 882Ԫ���൱��Ϊ16�ף���Ϊ10
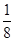 ��ʱ�������ͣ���������Ϊ38 882Ԫ��
��ʱ�������ͣ���������Ϊ38 882Ԫ��
��ϰ��ϵ�д�
�����Ŀ
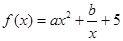
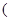 ����
����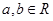 ������
������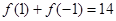 .
.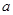 ��ֵ�����ͳ���
��ֵ�����ͳ���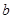 �IJ�ͬȡֵ���ۺ���
�IJ�ͬȡֵ���ۺ��� ��ż�ԣ�
��ż�ԣ�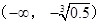 �ϵ����ݼ�����
�ϵ����ݼ�����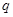 �Ҵ��ڵ���������������
�Ҵ��ڵ���������������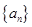 ��ʹ��
��ʹ��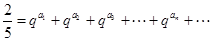 ����.
����. ,����a������ij���.
,����a������ij���. +
+ +��+
+��+ �����.
�����.  ��������ͬ�㴦�������غϣ������������Ϊ����
��������ͬ�㴦�������غϣ������������Ϊ���� ����
����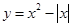 ����
����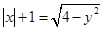 ����
���� ��Ӧ�������д��ڡ��Թ����ߡ����У� ��
��Ӧ�������д��ڡ��Թ����ߡ����У� ��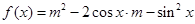 ��
��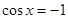 ʱȡ�����ֵ����
ʱȡ�����ֵ����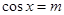 ʱȡ����Сֵ����ʵ��
ʱȡ����Сֵ����ʵ��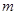 ��ȡֵ��ΧΪ�� ��
��ȡֵ��ΧΪ�� ��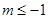
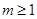
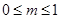
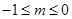
 (x)=��x(x+1)������g(x)=f(logax)(0��a��1)�ĵ����ݼ������ǣ� ��
(x)=��x(x+1)������g(x)=f(logax)(0��a��1)�ĵ����ݼ������ǣ� �� ��+��),(0,1]
��+��),(0,1]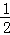 ��
�� �Ƕ�����
�Ƕ����� �ϵĺ������Ҷ�����ʵ��
�ϵĺ������Ҷ�����ʵ�� ������
������ ����
���� �Ľ⼯Ϊ ���� .
�Ľ⼯Ϊ ���� . ��
�� Ϊʵ��������
Ϊʵ�������� ������
������ ���������������ú��������ԵĶ�����ʵ��
���������������ú��������ԵĶ�����ʵ�� ��������ʽ
��������ʽ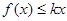 ��
��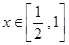 �н⣬��
�н⣬�� ��ȡֵ��Χ��
��ȡֵ��Χ��