题目内容
(本题满分14分)已知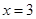 是函数
是函数 的一个极值点.
的一个极值点.
(Ⅰ)求 ;
;
(Ⅱ)求函数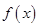 的单调区间;
的单调区间;
(Ⅲ)若直线 与函数
与函数 的图象有3个交点,求
的图象有3个交点,求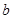 的取值范围.
的取值范围.
【答案】
(Ⅰ)
(Ⅱ)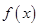 的单调增区间是
的单调增区间是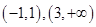 ,
,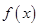 的单调减区间是
的单调减区间是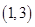
(Ⅲ)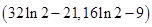 。
。
【解析】本试题主要是考查了导数在研究函数中的运用。利用导数求解参数的值,以及函数的单调区间,和函数与方程的关系的综合运用。
(1)由于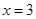 是函数
是函数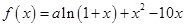 的一个极值点.,则说明在该点的导数值为零,得到参数a的值。
的一个极值点.,则说明在该点的导数值为零,得到参数a的值。
(2)然后利用第一问的结论,得到导数,结合导数的符号与单调性的关系,求解单调区间。
(3)分离函数的思想,研究两个图像的交点个数,即为方程解的问题的运用。
(Ⅰ)因为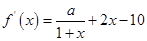
所以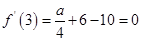
因此
(Ⅱ)由(Ⅰ)知,
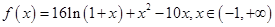
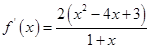
当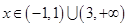 时,
时,
当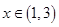 时,
时,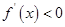
所以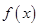 的单调增区间是
的单调增区间是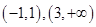
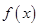 的单调减区间是
的单调减区间是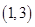
(Ⅲ)由(Ⅱ)知,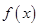 在
在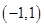 内单调增加,在
内单调增加,在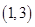 内单调减少,在
内单调减少,在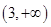 上单调增加,且当
上单调增加,且当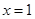 或
或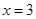 时,
时,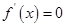
所以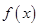 的极大值为
的极大值为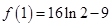 ,极小值为
,极小值为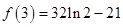
因此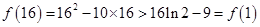
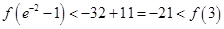
所以在 的三个单调区间
的三个单调区间 直线
直线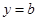 有
有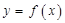 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当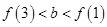
因此,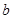 的取值范围为
的取值范围为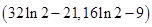 。
。

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目

 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
