题目内容
倾斜角为60°的直线l经过抛物线y2=2px(p>0)的焦点,且与抛物线相交于A,B两点(点A在x轴上方),则
的值为( )
| |AF| |
| |BF| |
分析:设抛物线y2=2px(p>0)的准线为l.如图所示,分别过点A,B作AM⊥l,BN⊥l,垂足为M,N.过点B作BC⊥AM交于点C.由抛物线的定义可得:|AM|=|AF|,|BN|=|BF|.由于AM∥x轴,∴∠BAC=∠AFx=60°.在Rt△ABC中,|AC|=
|AB|.化简即可得出.
| 1 |
| 2 |
解答:解:设抛物线y2=2px(p>0)的准线为l:x=-
.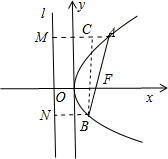
如图所示,分别过点A,B作AM⊥l,BN⊥l,垂足为M,N.
过点B作BC⊥AM交于点C.
则|AM|=|AF|,|BN|=|BF|.
∵AM∥x轴,
∴∠BAC=∠AFx=60°.
在Rt△ABC中,|AC|=
|AB|.
又|AM|-|BN|=|AC|,
∴|AF|-|BF|=
(|AF|+|BF|),
化为
=3.
故选:C.
| p |
| 2 |

如图所示,分别过点A,B作AM⊥l,BN⊥l,垂足为M,N.
过点B作BC⊥AM交于点C.
则|AM|=|AF|,|BN|=|BF|.
∵AM∥x轴,
∴∠BAC=∠AFx=60°.
在Rt△ABC中,|AC|=
| 1 |
| 2 |
又|AM|-|BN|=|AC|,
∴|AF|-|BF|=
| 1 |
| 2 |
化为
| |AF| |
| |BF| |
故选:C.
点评:本题考查了抛物线的定义、含60°角的直角三角形的性质、平行线的性质,考查了辅助线的作法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•闵行区二模)过坐标原点O作倾斜角为60°的直线交抛物线Γ:y2=x于P1点,过P1点作倾斜角为120°的直线交x轴于Q1点,交Γ于P2点;过P2点作倾斜角为60°的直线交x轴于Q2点,交Γ于P3点;过P3点作倾斜角为120°的直线,交x轴于Q3点,交Γ于P4点;如此下去….又设线段OQ1,Q1Q2,Q2Q3,…,Qn-1Qn,…的长分别为a1,a2,a3,…,an,…,数列{an}的前n项的和为Sn.
(2013•闵行区二模)过坐标原点O作倾斜角为60°的直线交抛物线Γ:y2=x于P1点,过P1点作倾斜角为120°的直线交x轴于Q1点,交Γ于P2点;过P2点作倾斜角为60°的直线交x轴于Q2点,交Γ于P3点;过P3点作倾斜角为120°的直线,交x轴于Q3点,交Γ于P4点;如此下去….又设线段OQ1,Q1Q2,Q2Q3,…,Qn-1Qn,…的长分别为a1,a2,a3,…,an,…,数列{an}的前n项的和为Sn.