题目内容
若点A的坐标为(3,2),F为抛物线y2=2x的焦点,点P是抛物线上的一动点,则|PA|+|PF|取得最小值时点P的坐标是( )
分析:利用抛物线的定义,将点P到其焦点的距离转化为它到其准线的距离即可.
解答:解:根据题意,作图如下,
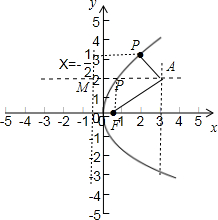
设点P在其准线x=-
上的射影为M,有抛物线的定义得:|PF|=|PM|,
∴欲使|PA|+|PF|取得最小值,就是使|PA|+|PM|最小,
∵|PA|+|PM|≥|AM|(当且仅当M,P,A三点共线时取“=”),
∴|PA|+|PF|取得最小值时(M,P,A三点共线时)点P的纵坐标y0=2,设其横坐标为x0,
∵P(x0,2)为抛物线y2=2x上的点,
∴x0=2,
∴点P的坐标为P(2,2).
故选C.
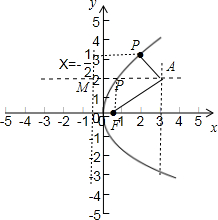
设点P在其准线x=-
| 1 |
| 2 |
∴欲使|PA|+|PF|取得最小值,就是使|PA|+|PM|最小,
∵|PA|+|PM|≥|AM|(当且仅当M,P,A三点共线时取“=”),
∴|PA|+|PF|取得最小值时(M,P,A三点共线时)点P的纵坐标y0=2,设其横坐标为x0,
∵P(x0,2)为抛物线y2=2x上的点,
∴x0=2,
∴点P的坐标为P(2,2).
故选C.
点评:本题考查抛物线的简单性质,将点P到其焦点的距离转化为它到其准线的距离是关键,考查转化思想的灵活应用,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
若点A的坐标为(3,2),F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为( )
| A、(0,0) | ||
B、(
| ||
C、(1,
| ||
| D、(2,2) |