题目内容
（2012•虹口区三模）对于直角坐标系内任意两点P1（x1，y1）、P2（x2，y2），定义运算：P1?P2=（x1，y1）?（x2，y2）=（x1x2-y1y2，x1y2+x2y1），若点M的坐标为（2，3），且M?（1，1）=N，则∠MON等于
．
| π |
| 4 |
| π |
| 4 |
分析：利用新定义求出N的坐标，通过向量的数量积求出所求的角即可．
解答：解：因为P1?P2=（x1，y1）?（x2，y2）=（x1x2-y1y2，x1y2+x2y1），
点M的坐标为（2，3），且M?（1，1）=N，
∴N=（2，3）?（1，1）=（-1，5）．
所以cos∠MON=
=
，
所以∠MON=
．
故答案为：
．
点M的坐标为（2，3），且M?（1，1）=N，
∴N=（2，3）?（1，1）=（-1，5）．
所以cos∠MON=
| -1×2+3×5 | ||||
|
| ||
| 2 |
所以∠MON=
| π |
| 4 |
故答案为：
| π |
| 4 |
点评：本题考查新定义的应用，数量积的应用，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
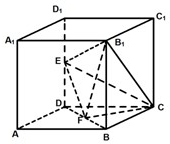（2012•虹口区三模）如图所示，在棱长为2的正方体ABCD-A1B1C1D1中，E、F分别为DD1、DB的中点．
（2012•虹口区三模）函数y=2x和y=x3的图象的示意图如图所示，设两函数的图象交于点A（x1，y1），B（x2，y2），且x1＜x2．