题目内容
已知数列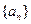 的前
的前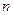 项和
项和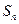 和通项
和通项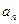 满足
满足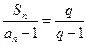 (
(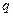 是常数且
是常数且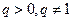 )。
)。
(Ⅰ)求数列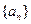 的通项公式;
的通项公式;
(Ⅱ) 当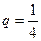 时,试证明
时,试证明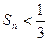 ;
;
 (Ⅲ)设函数
(Ⅲ)设函数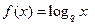 ,
,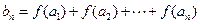 ,是否存在正整数
,是否存在正整数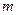 ,使
,使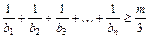 对
对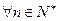 都成立?若存在,求出
都成立?若存在,求出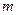 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
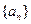 的前
的前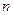 项和
项和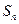 和通项
和通项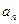 满足
满足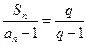 (
(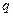 是常数且
是常数且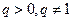 )。
)。(Ⅰ)求数列
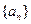 的通项公式;
的通项公式;(Ⅱ) 当
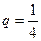 时,试证明
时,试证明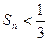 ;
; (Ⅲ)设函数
(Ⅲ)设函数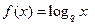 ,
,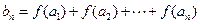 ,是否存在正整数
,是否存在正整数 ,使
,使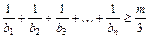 对
对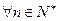 都成立?若存在,求出
都成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1)

(2)略
(3)1,2,3
解: (Ⅰ)由题意,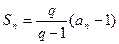 ,得
,得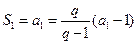
 ∴
∴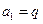 …………1分
…………1分
当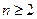 时,
时, 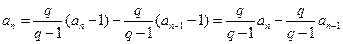 ,
,
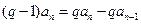 ∴
∴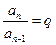 ………………3分
………………3分
∴数列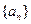 是首项
是首项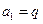 ,公比为
,公比为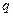 的等比数列,∴
的等比数列,∴ ………4分
………4分
(Ⅱ)由(Ⅰ)知当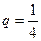 时,
时,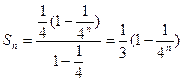 …………………5分
…………………5分
∵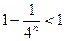 ,∴
,∴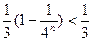 …………………………………………………6分
…………………………………………………6分
即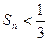 …………………………………………………………………………7分
…………………………………………………………………………7分
(Ⅲ)∵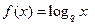
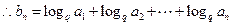 =
=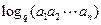
=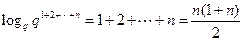 ……………………9分
……………………9分
∵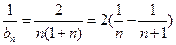 ………………………………10分
………………………………10分
∴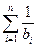
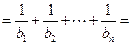
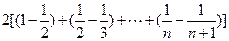 =
=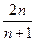 …12分
…12分
由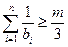 得
得
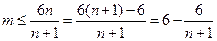 -------(
-------(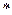 )
)
∵(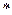 )对
)对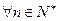 都成立 ∴
都成立 ∴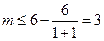 ∵
∵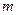 是正整数,∴
是正整数,∴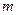 的值为1,2,3。
的值为1,2,3。
∴使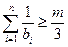 对
对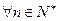 都成立的正整数
都成立的正整数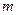 存在,其值为:1,2,3. …14分
存在,其值为:1,2,3. …14分
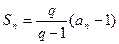 ,得
,得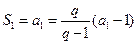
 ∴
∴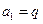 …………1分
…………1分当
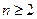 时,
时, 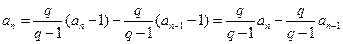 ,
,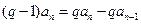 ∴
∴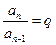 ………………3分
………………3分∴数列
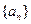 是首项
是首项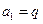 ,公比为
,公比为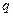 的等比数列,∴
的等比数列,∴ ………4分
………4分(Ⅱ)由(Ⅰ)知当
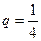 时,
时,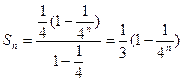 …………………5分
…………………5分∵
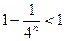 ,∴
,∴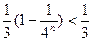 …………………………………………………6分
…………………………………………………6分即
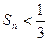 …………………………………………………………………………7分
…………………………………………………………………………7分(Ⅲ)∵
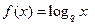
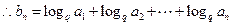 =
=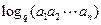
=
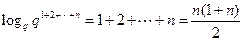 ……………………9分
……………………9分∵
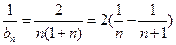 ………………………………10分
………………………………10分∴
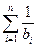
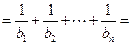
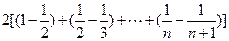 =
=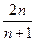 …12分
…12分由
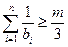 得
得
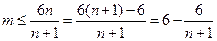 -------(
-------( )
)∵(
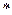 )对
)对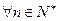 都成立 ∴
都成立 ∴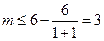 ∵
∵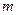 是正整数,∴
是正整数,∴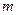 的值为1,2,3。
的值为1,2,3。∴使
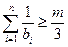 对
对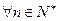 都成立的正整数
都成立的正整数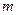 存在,其值为:1,2,3. …14分
存在,其值为:1,2,3. …14分
练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
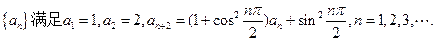
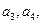 并求数列
并求数列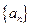 的通项公式;
的通项公式;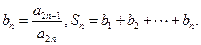 ,求
,求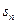 。
。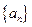 满足
满足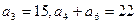 ,
,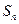 为
为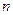 项和.
项和.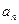 及当
及当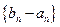 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列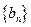 的通项公式及其前
的通项公式及其前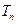 .
.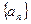 满足:
满足: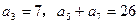 ,
,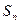 ,
,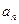 及
及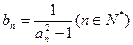 ,求数列
,求数列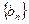 的前n项和
的前n项和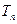 .
.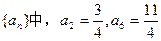
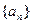 的通项公式;
的通项公式;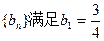 ,且
,且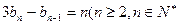 ),求证
),求证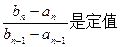 ;
;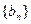 通项公式及前n项和
通项公式及前n项和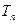 。
。 是边长为1的正三角形,曲线
是边长为1的正三角形,曲线 、
、 分别以
分别以 为圆心,
为圆心,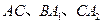 为半径画的弧,
为半径画的弧, 为曲线的第1圈,然后又以
为曲线的第1圈,然后又以 为圆心,
为圆心, 为半径画弧
为半径画弧 ,这样画到第
,这样画到第 圈,则所得曲
圈,则所得曲 的总长度
的总长度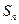 为 ( )
为 ( ) 








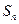 是等差数列
是等差数列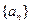 的前
的前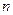 项和,且
项和,且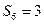 ,
,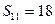 ,则
,则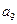 等于( )
等于( )