Question

在棱长为1的正方体ABCD-A₁B₁C₁D₁的底面A₁B₁C₁D₁上取一点E使AE与AB、AD所成的角都等于60°，则AE的长为．

• A．

  5

  2

• B．

  6

  2

• C．

  2

• D．

  3

Answer 1

分析：在正方体的对角面AA1C1C中，找到EH∥AA₁，从而EH⊥平面ABCD，AE在平面ABCD内的射影AH在正方形对角线AC上，从而AE满足与AB、AD所成的角相等．再作HI⊥AB于I，连接EI，设AI=x，利用解直角三角形，得AE=2x，AH=

2

x，最后在Rt△AEH中利用勾股定理，可建立等式，最终求出AE的长度．

解答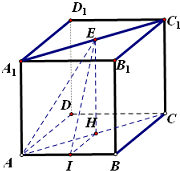：解：连接AC、A₁C₁，分别在A₁C₁、AC上取一点E、H，使AH=A₁E，连接AE、EH
过H作HI⊥AB于I，连接IE
∵多面体ABCD-A₁B₁C₁D₁是正方体
∴四边形AA₁C₁C是矩形
∴AH∥A₁E，再结合AH=A₁E
∴四边形AA₁EH是平行四边形
∴EH∥AA₁，再结合AA₁与平面ABCD垂直
∴EH⊥平面ABCD
∵AC是∠BAD的平分线，AE在底面ABCD内的射影AH在AC上
∴∠EAD=∠EAB
∵AB?平面ABCD，EH⊥平面ABCD
∴AB⊥EH，再结合AB⊥HI，EH∩HI=H
得：AB⊥平面EHI
∵EI?平面EHI
∴EI⊥AB
Rt△AEI中，设AI=x，∠EAI=60°
∴cos60°=

AI

AE

=

1

2

，可得AE=2x
Rt△AHI中，∠HAI=45°
∴cos45°=

AI

AH

=

2

2

，可得AH=

2

x
在Rt△AEH中，AH²+EH²=AE²
∴(

2

x)  2+1 2=(2x) 2，可得x=

2

2

∴AE=2x=

2

故选C

点评：本题考查了空间距离的计算，属于中档题．解题过程中用到了直线与平面垂直的判定与性质，请同学们注意从“线面垂直”到“线线垂直”的互相转化．