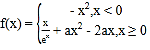题目内容
【题目】如图:在五面体![]() 中,四边形
中,四边形![]() 是正方形,
是正方形,![]() ,
,![]() ,
,
![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】分析:第一问证明面面垂直,在证明的过程中,利用常规方法,抓住面面垂直的判定定理,找出相应的垂直关系证得结果,第二问求的是线面角的正弦值,利用空间向量,将其转化为直线的方向向量与平面的法向量所成角的余弦值的绝对值,从而求得结果.
详解:(1)证明:因为![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() .
.
(2)解:由已知![]() ,所以
,所以![]() 平面
平面![]() .
.
又平面![]() 平面
平面![]() ,故
,故![]() .
.
所以四边形![]() 为等腰梯形.
为等腰梯形.
又![]() ,所以
,所以![]() ,易得
,易得![]() ,令
,令![]() ,
,
如图,以![]() 为原点,以
为原点,以![]() 的方向为
的方向为![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由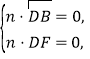
所以 取
取![]() ,则
,则![]() ,
,![]() ,得
,得![]() ,
,
 .
.
设直线与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


【题目】基于移动互联技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验![]() 某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月内的市场占有率进行了统计,结果如下表:
某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月内的市场占有率进行了统计,结果如下表:
月份 |
|
|
|
|
|
|
月份代码x | 1 | 2 | 3 | 4 | 5 | 6 |
市场占有率 | 11 | 13 | 16 | 15 | 20 | 21 |
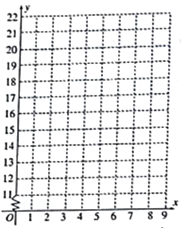
![]() 请在给出的坐标纸中作出散点图,并用相关系数说明可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系;
请在给出的坐标纸中作出散点图,并用相关系数说明可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系;
![]() 求y关于x的线性回归方程,并预测该公司2018年2月份的市场占有率;
求y关于x的线性回归方程,并预测该公司2018年2月份的市场占有率;
![]() 根据调研数据,公司决定再采购一批单车扩大市场,现有采购成本分别为1000元
根据调研数据,公司决定再采购一批单车扩大市场,现有采购成本分别为1000元![]() 辆和800元
辆和800元![]() 辆的A,B两款车型报废年限各不相同
辆的A,B两款车型报废年限各不相同![]() 考虑到公司的经济效益,该公司决定先对两款单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
考虑到公司的经济效益,该公司决定先对两款单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
报废年限 车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
A | 10 | 30 | 40 | 20 | 100 |
B | 15 | 40 | 35 | 10 | 100 |
经测算,平均每辆单车每年可以为公司带来收入500元![]() 不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且用频率估计每辆单车使用寿命的概率,以每辆单车产生利润的期望值为决策依据
不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且用频率估计每辆单车使用寿命的概率,以每辆单车产生利润的期望值为决策依据![]() 如果你是该公司的负责人,你会选择采购哪款车型?
如果你是该公司的负责人,你会选择采购哪款车型?
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数![]() ,
,
回归直线方程为![]() 其中:
其中:![]() ,
,![]() .
.