题目内容
(本题满分13分)设数列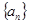 为单调递增的等差数列
为单调递增的等差数列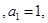 且
且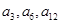 依次成等比数列.
依次成等比数列.
(Ⅰ)求数列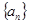 的通项公式
的通项公式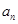 ;
;
(Ⅱ)若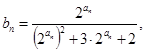 求数列
求数列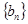 的前
的前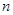 项和
项和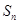 ;
;
(Ⅲ)若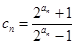 ,求证:
,求证: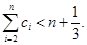
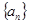 为单调递增的等差数列
为单调递增的等差数列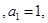 且
且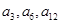 依次成等比数列.
依次成等比数列.(Ⅰ)求数列
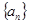 的通项公式
的通项公式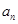 ;
;(Ⅱ)若
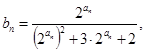 求数列
求数列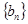 的前
的前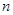 项和
项和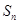 ;
;(Ⅲ)若
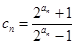 ,求证:
,求证: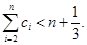
(1)
(2)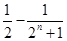
(3)根据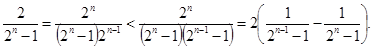 ,放缩来求和得到证明。
,放缩来求和得到证明。

(2)
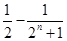
(3)根据
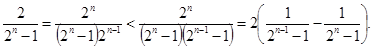 ,放缩来求和得到证明。
,放缩来求和得到证明。试题分析:解:⑴
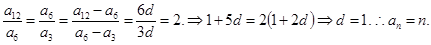 …3分
…3分⑵
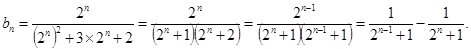
则
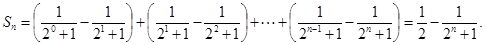 …7分
…7分⑶

而
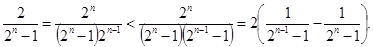
所以
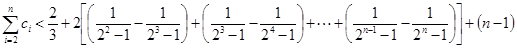
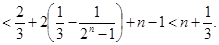 …………………….13分
…………………….13分点评:解决该试题最重要的是第一步中通项公式的求解,利用等差数列的通项公式,得到数列
 ,然后利用裂项求和得到第二问,裂项法是求和中重要而又常用 方法之一。同时能借助于放缩法得到不等式的证明。第三问是个难点。
,然后利用裂项求和得到第二问,裂项法是求和中重要而又常用 方法之一。同时能借助于放缩法得到不等式的证明。第三问是个难点。
练习册系列答案
相关题目
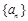 中,如果对任意的
中,如果对任意的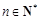 ,都有
,都有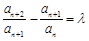 (
(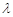 为常数),则称数列
为常数),则称数列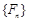 满足
满足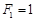 ,
,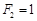 ,
,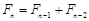 (
(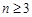 ),则该数列不是比等差数列;②若数列
),则该数列不是比等差数列;②若数列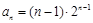 ,则数列
,则数列 ;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若
;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若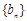 是等比数列,则数列
是等比数列,则数列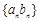 是比等差数列.
是比等差数列.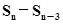 =51(n>3) ,
=51(n>3) ,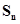 = 100,则n的值为
= 100,则n的值为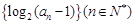 为等差数列,且
为等差数列,且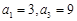
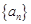 的通项公式;
的通项公式;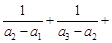 …
…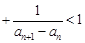 .
.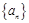 是各项均不为
是各项均不为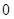 的等差数列,公差为
的等差数列,公差为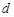 ,
,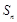 为其前
为其前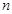 项和,且满足
项和,且满足 ,
,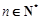 .数列
.数列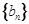 满足
满足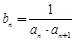 ,
,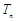 为数列
为数列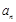 和数列
和数列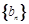 的前n项和
的前n项和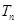 ;
;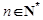 ,不等式
,不等式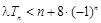 恒成立,求实数
恒成立,求实数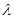 的取值范围;
的取值范围;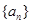 前
前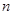 项和
项和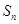 满足
满足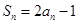 ,等差数列
,等差数列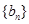 满足
满足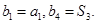
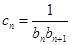 ,数列
,数列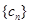 的前
的前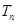 ,问
,问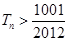 的最小正整数n是多少?
的最小正整数n是多少?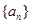 的前
的前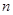 项和
项和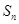 和通项
和通项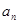 满足
满足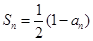 .
.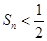 ;
;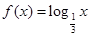 ,
,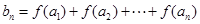 ,求
,求 .
.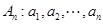 ,(例如
,(例如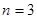 时,
时,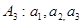 )满足
)满足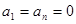 ,且当
,且当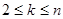 (
(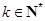 )时,
)时,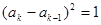 .令
.令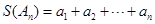 .
.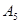 的所有可能的情况;(5分)
的所有可能的情况;(5分)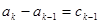 ,求
,求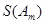 (用
(用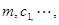
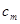 的代数式来表示);(5分)
的代数式来表示);(5分)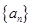 中,
中, 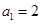 ,
,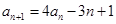 ,
,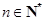 .
.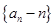 是等比数列;
是等比数列;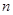 项和
项和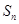 .
.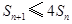 成立.
成立.