题目内容
(2012•江西)(1)(坐标系与参数方程选做题)曲线C的直角坐标方程为x2+y2-2x=0,以原点为极点,x轴的正半轴为极轴建立积坐标系,则曲线C的极坐标方程为
(2)(不等式选做题)在实数范围内,不等式|2x-1|+|2x+1|≤6的解集为
ρ=2cosθ
ρ=2cosθ
.(2)(不等式选做题)在实数范围内,不等式|2x-1|+|2x+1|≤6的解集为
{x|-
≤ x≤
}
| 3 |
| 2 |
| 3 |
| 2 |
{x|-
≤ x≤
}
.| 3 |
| 2 |
| 3 |
| 2 |
分析:(1)利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得
(2)利用绝对值的几何意义求解.
(2)利用绝对值的几何意义求解.
解答: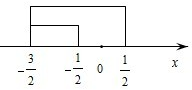 解:(1)利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换,得出ρ2-2ρcosθ=0.即ρ=2cosθ
解:(1)利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换,得出ρ2-2ρcosθ=0.即ρ=2cosθ
故答案为:ρ=2cosθ
(2)不等式|2x-1|+|2x+1|≤6化为不等式|x-
|+|x+
|≤3,如图所示
数轴上点-
,
到点
,-
的距离之和为3,所以解集为{x|-
≤ x≤
}
故答案为:{x|-
≤ x≤
}
 解:(1)利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换,得出ρ2-2ρcosθ=0.即ρ=2cosθ
解:(1)利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换,得出ρ2-2ρcosθ=0.即ρ=2cosθ故答案为:ρ=2cosθ
(2)不等式|2x-1|+|2x+1|≤6化为不等式|x-
| 1 |
| 2 |
| 1 |
| 2 |
数轴上点-
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:{x|-
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查极坐标和直角坐标的互化,绝对值不等式求解,其中(2)利用了绝对值的几何意义,避免了分类讨论.

练习册系列答案
相关题目

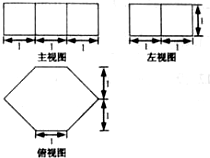 (2012•江西)若一个几何体的三视图如图所示,则此几何体的体积为( )
(2012•江西)若一个几何体的三视图如图所示,则此几何体的体积为( ) (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2012•江西模拟)函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,
(2012•江西模拟)函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,