题目内容
3.已知φ,β均为锐角,cosφ=$\frac{3}{5}$,cos(φ+β)=-$\frac{5}{13}$,求cosβ的值.分析 求出sinφ,sin(φ+β),然后求解cosβ的值.
解答 解:φ,β均为锐角,cosφ=$\frac{3}{5}$,sinφ=$\frac{4}{5}$.
cos(φ+β)=-$\frac{5}{13}$,sin(φ+β)=$\sqrt{1-(-\frac{5}{13})^{2}}$=$\frac{12}{13}$.
cosβ=cos[(φ+β)-φ]=cos(φ+β)cosφ+sin(φ+β)sinφ=$-\frac{5}{13}×\frac{3}{5}+\frac{12}{13}×\frac{4}{5}$=$\frac{33}{65}$.
点评 本题考查两角和与差的余弦函数的应用,考查计算能力.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
18.某几何体在网格纸上的三视图如图所示,已知网格纸上小正方形的边长为1,则该几何体的体积为( )
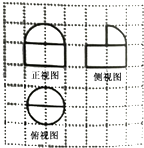

| A. | $\frac{4π}{3}$ | B. | $\frac{5π}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |
12.已知函数f(x)=$\left\{\begin{array}{l}{-lnx,0<x≤e}\\{a(x+e),x>e}\end{array}\right.$是(0,+∞)上的减函数,且对任意m∈(0,e],n∈(e,+∞)有f($\frac{m+n}{2}$)$<\frac{1}{2}$[f(m)+f(n)],那么实数a的取值范围是( )
| A. | a<-$\frac{1}{e}$ | B. | a$≤-\frac{1}{2e}$ | C. | -1≤a<0 | D. | -$\frac{1}{e}$<a≤-$\frac{1}{2e}$ |