题目内容
14．六个人排成一排照相，其中甲不站在两端的排法种数为480．分析 根据题意，假设6个人分别对应6个空位，甲不站在两端，有4个位置可选；而其他5人对应其他5个位置，对其全排列，可得其排法数目，由分步计数原理计算可得答案．
解答 解：假设6个人分别对应6个空位，甲不站在两端，有4个位置可选；
则其他5人对应其他5个位置，有A55=120种情况，
则不同排列方法种数4×120=480种．
故答案为：480．
点评 本题考查排列、组合的运用，一般要先处理特殊（受到限制的）元素．
练习册系列答案
相关题目
4．一枚质地均匀的正方体骰子，六个面上分别刻着1点至6点．甲、乙二人各掷骰子一次，则甲掷得的向上的点数比乙大的概率为（ ）
| A． | $\frac{2}{9}$ | B． | $\frac{1}{4}$ | C． | $\frac{5}{12}$ | D． | $\frac{1}{2}$ |
5．
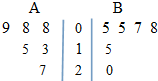某普通高中共有36个班，每班40名学生，每名学生都有且只有一部手机，为了解该校学生对A，B两种品牌手机的持有率及满意度情况，校学生会随机抽取了该校6个班的学生进行统计，得到每班持有两种品牌手机人数的茎叶图以及这些学生对自己所持手机的满意度统计表如下：
（Ⅰ）随机选取1名该校学生，估计该生持有A品牌手机的概率；
（Ⅱ）随机选取1名该校学生，估计该生持有A或B品牌手机且感到满意的概率；
（Ⅲ）A，B两种品牌的手机哪种市场前景更好？（直接写出结果，不必证明）
某普通高中共有36个班，每班40名学生，每名学生都有且只有一部手机，为了解该校学生对A，B两种品牌手机的持有率及满意度情况，校学生会随机抽取了该校6个班的学生进行统计，得到每班持有两种品牌手机人数的茎叶图以及这些学生对自己所持手机的满意度统计表如下：满意度 品牌 | 满意 | 不满意 |
| A | 80% | 20% |
| B | 60% | 40% |
（Ⅱ）随机选取1名该校学生，估计该生持有A或B品牌手机且感到满意的概率；
（Ⅲ）A，B两种品牌的手机哪种市场前景更好？（直接写出结果，不必证明）
2．若实数x，y满足不等式组$\left\{\begin{array}{l}{2x+y+2≥0}\\{x+y-1≤0}\\{y≥0}\end{array}\right.$，则z=y-2x的最小值等于（ ）
| A． | 1 | B． | 2 | C． | -1 | D． | -2 |
19．设变量x，y满足约束条件$\left\{\begin{array}{l}{x+y-4≤0}\\{x+y-2≤0}\\{x≥0}\end{array}\right.$，则目标函数z=2x+3y的最大值为（ ）
| A． | 9 | B． | 10 | C． | 11 | D． | 12 |
6．
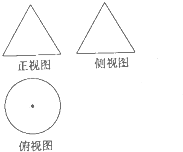如图是一个空间几何体的三视图（注：正视图也称主视图，侧视图也称左视图），其中正视图和侧视图都是边长为6的正三角形，俯视图是直径等于6的圆，则这个空间几何体的体积为（ ）
如图是一个空间几何体的三视图（注：正视图也称主视图，侧视图也称左视图），其中正视图和侧视图都是边长为6的正三角形，俯视图是直径等于6的圆，则这个空间几何体的体积为（ ）| A． | 54π | B． | 18π | C． | 9$\sqrt{3}π$ | D． | $\frac{\sqrt{3}π}{3}$ |
3．若实数x，y满足不等式组$\left\{\begin{array}{l}{2x+y+2≥0}\\{x+y+m≤0}\\{y≥0}\end{array}\right.$，且z=y-2x的最小值等于-2，则实数m的值等于（ ）
| A． | -1 | B． | 1 | C． | -2 | D． | 2 |
4．数列{an}中，若a1=$\frac{1}{2}$，an=$\frac{1}{1-{a}_{n-1}}$，（n≥2，n∈N），则a11的值为（ ）
| A． | -1 | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |