题目内容
设函数f(x)=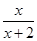 (x>0)
(x>0)
观察:f1(x)=f(x)=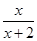 ,f2(x)=f(f1(x))=
,f2(x)=f(f1(x))=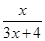 ,f3(x)=f(f2(x))=
,f3(x)=f(f2(x))=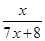 ,
,
f4(x)=f(f3(x))=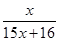 , 根据以上事实,由归纳推理可得:
, 根据以上事实,由归纳推理可得:
当n∈N*且n≥2时,fn(x)=f(fn-1(x))=________.
fn(x)=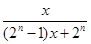
解析试题分析:由题知,fn(x)解析式是分式,其分子是 不变,分母是一次函数,当n=1,2,3,4时,
不变,分母是一次函数,当n=1,2,3,4时, 的系数分别为1,3,7,16,故
的系数分别为1,3,7,16,故 的系数为
的系数为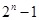 ,常数项为
,常数项为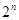 ,所以fn(x)=
,所以fn(x)=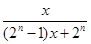 .
.
考点:归纳推理

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
将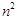 个正整数
个正整数 、
、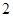 、
、 、…、
、…、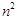 (
(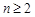 )任意排成
)任意排成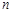 行
行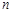 列的数表.对于某一个数表,计算各行和各列中的任意两个数
列的数表.对于某一个数表,计算各行和各列中的任意两个数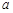 、
、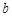 (
(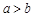 )的比值
)的比值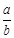 ,称这些比值中的最小值为这个数表的“特征值”.当
,称这些比值中的最小值为这个数表的“特征值”.当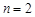 时, 数表的所有可能的“特征值”最大值为
时, 数表的所有可能的“特征值”最大值为
A. | B.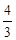 | C.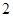 | D.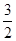 |
用反证法证明“如果a>b,那么 >
> ”假设的内容应是( )
”假设的内容应是( )
A. = = | B. < < |
C. = = 且 且 < < | D. = = 或 或 < < |
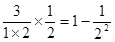 ; ?
; ? ;
; ,
, 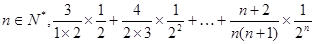 = .
= .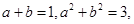
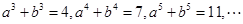 ,则依次类推可得
,则依次类推可得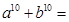 ;
;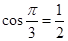


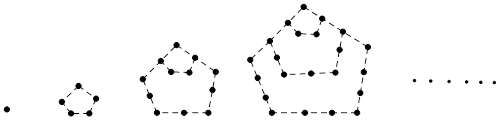
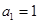 ,第2个五角形数记作
,第2个五角形数记作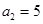 ,第3个五角形数记作
,第3个五角形数记作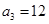 ,第4个五角形数记作
,第4个五角形数记作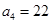 , ,若按此规律继续下去,则
, ,若按此规律继续下去,则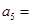 ,若
,若 ,则
,则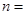 .
.

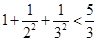

 的三边长分别为
的三边长分别为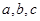 ,
,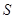 ,内切圆半径为
,内切圆半径为 ,则
,则 ;类比这个结论可知:四面体
;类比这个结论可知:四面体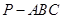 的四个面的面积分别为
的四个面的面积分别为 ,内切球的半径为
,内切球的半径为 ,四面体
,四面体 ,则
,则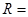 .
.