题目内容
设 的三边长分别为
的三边长分别为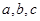 ,
, 的面积为
的面积为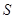 ,内切圆半径为
,内切圆半径为 ,则
,则 ;类比这个结论可知:四面体
;类比这个结论可知:四面体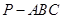 的四个面的面积分别为
的四个面的面积分别为 ,内切球的半径为
,内切球的半径为 ,四面体
,四面体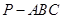 的体积为
的体积为 ,则
,则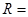 .
.
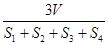
解析试题分析:三角形中,内切圆的圆心,与其三个顶点的连线,构成了三个小的三角形,并且有相同的高 ,底边分别是
,底边分别是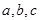 ,利用等面积法,我们得到
,利用等面积法,我们得到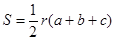 ,所以
,所以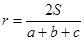 ;利用类比推理可知,在四面体内切球半径为
;利用类比推理可知,在四面体内切球半径为 ,四个面的面积分别为
,四个面的面积分别为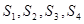 ,内切球的球心与各顶点的连线,将一个四面体分割为四个小的四面体,以四面体的四个面为底面,高都为
,内切球的球心与各顶点的连线,将一个四面体分割为四个小的四面体,以四面体的四个面为底面,高都为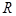 的四面体,由等体积法,可得到
的四面体,由等体积法,可得到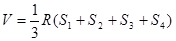 ,所以
,所以 .
.
考点:合情推理中的类比推理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某公司推出了下表所示的QQ在线等级制度,设等级为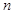 级需要的天数为
级需要的天数为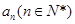 ,
,
| 等级 | 等级图标 | 需要天数 | 等级 | 等级图标 | 需要天数 |
| 1 |  | 5 | 7 |     | 77 |
| 2 |   | 12 | 8 |   | 96 |
| 3 |    | 21 | 12 |    | 192 |
| 4 |  | 32 | 16 |  | 320 |
| 5 |   | 45 | 32 |   | 1152 |
| 6 |    | 60 | 48 |    | 2496 |
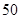 级需要的天数
级需要的天数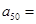 __________
__________ 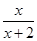 (x>0)
(x>0)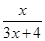 ,f3(x)=f(f2(x))=
,f3(x)=f(f2(x))=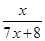 ,
,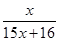 , 根据以上事实,由归纳推理可得:
, 根据以上事实,由归纳推理可得: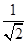 <1;②
<1;②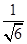 <
< ;③
;③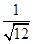 <
<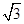 ;….则第n个不等式为________.
;….则第n个不等式为________.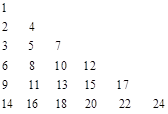
 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数,如
个数,如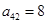 .若
.若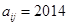 ,则
,则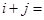 .
.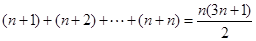
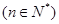 的第二步中,当
的第二步中,当 时等式左边与
时等式左边与 时的等式左边的差等于 .
时的等式左边的差等于 .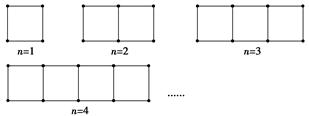
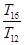 成等比数列.
成等比数列.