题目内容
将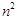 个正整数
个正整数 、
、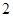 、
、 、…、
、…、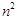 (
(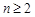 )任意排成
)任意排成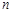 行
行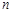 列的数表.对于某一个数表,计算各行和各列中的任意两个数
列的数表.对于某一个数表,计算各行和各列中的任意两个数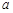 、
、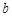 (
(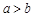 )的比值
)的比值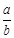 ,称这些比值中的最小值为这个数表的“特征值”.当
,称这些比值中的最小值为这个数表的“特征值”.当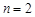 时, 数表的所有可能的“特征值”最大值为
时, 数表的所有可能的“特征值”最大值为
A. | B.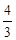 | C.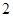 | D.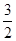 |
D
解析试题分析:当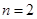 时,这4个数分别为1、2、3、4,排成了两行两列的数表,当
时,这4个数分别为1、2、3、4,排成了两行两列的数表,当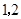 同行或同列时,这个数表的“特征值”为
同行或同列时,这个数表的“特征值”为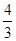 ;当
;当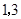 同行或同列时,这个数表的特征值分别为
同行或同列时,这个数表的特征值分别为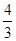 或
或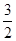 ;当
;当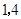 同行或同列时,这个数表的“特征值”为
同行或同列时,这个数表的“特征值”为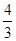 或
或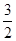 ;故这些可能的“特征值”的最大值为
;故这些可能的“特征值”的最大值为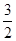
考点:1、计数原理;2、归纳推理.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
设 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且 满足:“当
满足:“当 成立时,总可推出
成立时,总可推出 成立”,那么,下列命题总成立的是 ( )
成立”,那么,下列命题总成立的是 ( )
A.若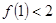 成立,则 成立,则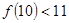 成立 成立 |
B.若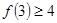 成立,则当 成立,则当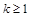 时,均有 时,均有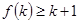 成立 成立 |
C.若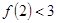 成立,则 成立,则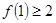 成立 成立 |
D.若 成立,则当 成立,则当 时,均有 时,均有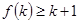 成立 成立 |
下列推理合理的是( )
A.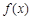 是增函数,则 是增函数,则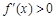 |
B.因为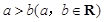 ,则 ,则 |
C.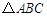 为锐角三角形,则 为锐角三角形,则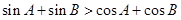 |
D.直线 ,则 ,则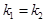 |
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线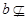 平面
平面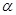 ,直线
,直线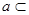 平面
平面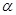 ,直线
,直线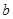 ∥平面
∥平面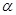 ,则直线
,则直线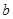 ∥直线
∥直线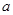 ”的结论显然是错误的,这是因为 ( )
”的结论显然是错误的,这是因为 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
用反证法证明命题:“a,b∈N,ab可被5整除,那么a,b中至少有一个能被5整除”时,假设的内容应为( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b不都能被5整除 | D.a不能被5整除 |
分析法是从要证明的结论出发,逐步寻求使结论成立的( )
| A.充分条件 | B.必要条件 | C.充要条件 | D.等价条件 |
已知f(x+1)= ,f(1)=1(x∈N*),猜想f(x)的表达式为( )
,f(1)=1(x∈N*),猜想f(x)的表达式为( )
A.f(x)= | B.f(x)= |
C.f(x)= | D.f(x)= |
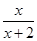 (x>0)
(x>0)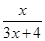 ,f3(x)=f(f2(x))=
,f3(x)=f(f2(x))=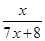 ,
,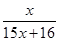 , 根据以上事实,由归纳推理可得:
, 根据以上事实,由归纳推理可得: =c+d
=c+d