题目内容
如图所示,直棱柱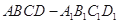 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, .
.
(1)求证: 平面
平面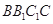 ;
;
(2)在A1B1上是否存一点 ,使得
,使得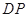 与平面
与平面 平行?证明你的结论.
平行?证明你的结论.
(1)证明略 (2)略
解析

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
题目内容
如图所示,直棱柱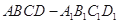 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, .
.
(1)求证: 平面
平面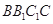 ;
;
(2)在A1B1上是否存一点 ,使得
,使得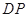 与平面
与平面 平行?证明你的结论.
平行?证明你的结论.
(1)证明略 (2)略
解析

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案