题目内容
9.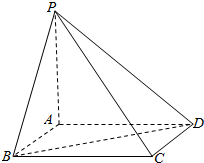 在四棱锥P-ABCD中:ABCD是正方形,PA⊥平面ABCD,PA=AB=a.
在四棱锥P-ABCD中:ABCD是正方形,PA⊥平面ABCD,PA=AB=a.(1)求二面角P-CD-A的大小;
(2)求四棱锥P-ABCD的全面积;
(3)求C点到平面PBD的距离.
分析 (1)找出二面角P-CD-A的平面角并求出大小;
(2)计算四棱锥P-ABCD各个面的面积再求和;
(3)利用等体积法即可求出C点到平面PBD的距离.
解答 解:(1)因为ABCD是正方形,PA⊥底面ABCD,所以PA⊥CD;
又CD⊥AD,所以CD⊥平面PAD,
所以PD⊥CD,AD⊥CD,
所以∠PDA为二面角P-CD-A的平面角,
又PA=AD=a,所以∠PDA=45°,
即二面角P-CD-A的大小为45°;
(2)由(1)得,CD⊥平面PAD,
所以CD⊥PD,△PCD是直角三角形;
因为PA=AB=a,所以S△PCD=$\frac{1}{2}$•a•$\sqrt{2}$a=$\frac{\sqrt{2}}{2}$a2;
同理CB⊥PB,即S△BCP=$\frac{\sqrt{2}}{2}$a2;
因为PA⊥面ABCD,底面ABCD为正方形,
所以S△ABP=S△ADP=$\frac{1}{2}$•a•a=$\frac{1}{2}$a2,
S底面ABCD=a2;
所以四棱锥P-ABCD的全面积为
S=$\frac{\sqrt{2}}{2}$a2+$\frac{\sqrt{2}}{2}$a2+$\frac{1}{2}$a2+$\frac{1}{2}$a2+a2=($\sqrt{2}$+2)a2;
(3)设C点到平面PBD的距离为h,
则△PBC是边长为$\sqrt{2}$a的正三角形,其面积为$\frac{\sqrt{3}}{4}$•${(\sqrt{2}a)}^{2}$=$\frac{\sqrt{3}}{2}$a2;
所以三棱锥P-BDC的体积是
V三棱锥P-BDC=$\frac{1}{3}$×$\frac{1}{2}$a2×a=$\frac{1}{3}$×$\frac{\sqrt{3}}{2}$a2•h,
解得h=$\frac{\sqrt{3}}{3}$a,
即C点到平面PBD的距离为$\frac{\sqrt{3}}{3}$a.
点评 本题考查了三棱锥中线面角以及面面角的求法以及点到平面距离的计算问题,考查了空间想象能力与转化思想的应用问题,是综合性题目.

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
| A. | S△AOC的最小值为$\frac{1}{2}$S | B. | SAOB的最小值为($\sqrt{2}$-1)S | ||
| C. | S△AOC+S△AOB的最大值为$\frac{1}{2}$S | D. | S△BOC的最大值为($\sqrt{2}$-1)S |
 如图所示数阵,记an为数字n的个数,记An为an个数字n的和.已知数列{bn}满足bn=$\frac{1}{{A}_{n}+5n}$,Bn为数列{bn}的前n项和,且Bn<t恒成立.
如图所示数阵,记an为数字n的个数,记An为an个数字n的和.已知数列{bn}满足bn=$\frac{1}{{A}_{n}+5n}$,Bn为数列{bn}的前n项和,且Bn<t恒成立. 如图,长方体ABCD-A1B1C1D1的底面边长均为1,侧棱AA1=2,M,N分别是A1C1,A1A的中点,
如图,长方体ABCD-A1B1C1D1的底面边长均为1,侧棱AA1=2,M,N分别是A1C1,A1A的中点,