题目内容
1.设函数f(x)=x•1nx,g(x)=ax2-2ax+1.(1)求函数f(x)的单调区间;
(2)若x∈[1,2],a∈[1,2],求证:f(x)≥g(x).
分析 (1)求导f′(x)=1+1nx,从而由导数的正负确定函数的单调性;
(2)构造函数F(x)=f(x)-g(x)=x•1nx-ax2+2ax-1,从而求导F′(x)=1+lnx-2ax+2a,F″(x)=$\frac{1}{x}$-2a,从而确定函数的最小值即可.
解答 解:(1)∵f(x)=x•1nx,f′(x)=1+1nx,
故当x∈(0,$\frac{1}{e}$)时,f′(x)<0;
当x∈($\frac{1}{e}$,+∞)时,f′(x)>0;
故f(x)的单调减区间为(0,$\frac{1}{e}$),
单调增区间为($\frac{1}{e}$,+∞);
(2)证明:令F(x)=f(x)-g(x)=x•1nx-ax2+2ax-1,
故F′(x)=1+lnx-2ax+2a,F″(x)=$\frac{1}{x}$-2a,
∵x∈[1,2],a∈[1,2],
∴F″(x)=$\frac{1}{x}$-2a<0,
∴F′(x)在[1,2]上是减函数,
又∵F′(1)=1+0=1>0,F′(2)=1+ln2-4a+2a=1+ln2-2a<0,
∴F(x)在[1,2]上先增后减,
故F(x)的最小值在x=1或x=2上取得,
而F(1)=1ln1-a+2a-1=a-1≥0,(a∈[1,2]);
F(2)=2ln2-4a+4a-1=2ln2-1=ln4-1>0,
故F(x)≥0恒成立,即f(x)≥g(x).
点评 本题考查了导数的综合应用及恒成立问题与函数思想的应用.构造函数F(x)=f(x)-g(x)是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知f(x)=$\left\{\begin{array}{l}{(6-a)x-4a,x<1}\\{lo{g}_{a}x,x≥1}\end{array}\right.$在区间(-∞,+∞)上是单调递增函数,则实数a的取值范围是( )
| A. | (1,6) | B. | [$\frac{6}{5}$,6) | C. | [1,$\frac{6}{5}$] | D. | (1,+∞) |
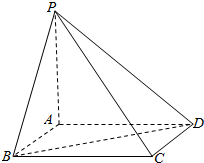 在四棱锥P-ABCD中:ABCD是正方形,PA⊥平面ABCD,PA=AB=a.
在四棱锥P-ABCD中:ABCD是正方形,PA⊥平面ABCD,PA=AB=a.