题目内容
若不等式|8x+9|<7和不等式ax2+bx>2的解集相等,则实数a、b的值分别为( )
| A.a=-8,b=-10 |
| B.a=-4,b=-9 |
| C.a=-1,b=9 |
| D.a=-1,b=2 |
B
根据题意可得|8x+9|<7⇒-2<x< ,
,
故由{x|-2<x< }是不等式ax2+bx>2的解集可知x1=-2,x2=
}是不等式ax2+bx>2的解集可知x1=-2,x2=
是一元二次方程ax2+bx-2=0的两根,根据根与系数的关系可知x1x2=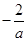 =
=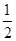 ⇒a=-4,x1+x2=
⇒a=-4,x1+x2=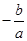 =
=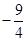 ⇒b=-9,故选B.
⇒b=-9,故选B.
 ,
,故由{x|-2<x<
 }是不等式ax2+bx>2的解集可知x1=-2,x2=
}是不等式ax2+bx>2的解集可知x1=-2,x2=
是一元二次方程ax2+bx-2=0的两根,根据根与系数的关系可知x1x2=
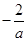 =
=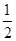 ⇒a=-4,x1+x2=
⇒a=-4,x1+x2=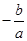 =
=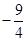 ⇒b=-9,故选B.
⇒b=-9,故选B.
练习册系列答案
相关题目
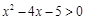 的解集是( )
的解集是( )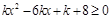 对任意
对任意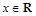 恒成立,则实数
恒成立,则实数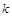 的取值范围为 .
的取值范围为 . ,则a-b=________.
,则a-b=________.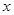 的不等式
的不等式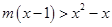 的解集为
的解集为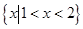 ,则实数
,则实数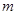 的值为 .
的值为 .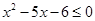 的解集为____________.
的解集为____________.