题目内容
若抛物线y2=ax上恒有关于直线x+y-1=0对称的两点A,B,则a的取值范围是( )
A.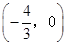 |
B.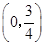 |
C.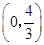 |
D.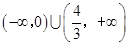 |
C
试题分析:设A(
 ,
,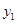 ),B(
),B(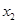 ,
,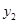 ),
),因为点A和B在抛物线上,所以有
 =a
=a ①
①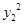 =a
=a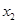 ②
②①-②得,
 ?
? 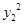 =a(
=a( ?
? 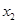 ).
).整理得
 ,
,因为A,B关于直线x+y-1=0对称,所以
 =1,即
=1,即 =1.
=1.所以
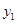 +
+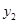 =a.
=a.设AB的中点为M(x0,y0),则y0=
 .
.又M在直线x+y-1=0上,所以x0=1?y0=1?
 .
.则M(1?
 ,
, ).
).因为M在抛物线内部,所以
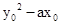 <0.
<0.即
 <0,解得0<a<
<0,解得0<a< .故选C.
.故选C.点评:中档题,“点差法”是解决与弦中点有关问题的常用方法,解答的关键是由AB中点在抛物线内部得到关于a的不等式.

练习册系列答案
相关题目
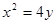 的焦点为
的焦点为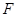 ,过
,过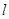 (
(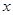 轴不平行)交抛物线分别于
轴不平行)交抛物线分别于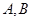 两点,点
两点,点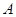 关于
关于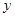 轴对称点为
轴对称点为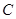 ,
,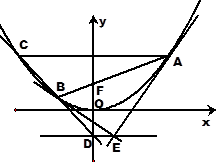
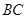 与
与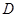 必为定点;
必为定点;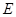 ,求
,求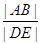 的最小值,并求当
的最小值,并求当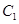 ,抛物线
,抛物线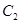 的焦点均在
的焦点均在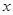 轴上,
轴上,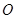 ,每条曲线上取两个点,将其坐标记录于表中:
,每条曲线上取两个点,将其坐标记录于表中:
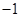
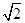
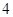
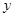
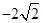
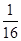
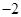
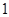
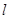 与
与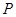 ,且与
,且与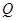 ,试探究:在坐标平面内是否存在定点
,试探究:在坐标平面内是否存在定点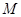 ,使得以
,使得以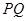 为直径的圆恒过点
为直径的圆恒过点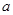 ,则M到y轴距离为 ( )
,则M到y轴距离为 ( )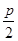
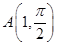 ,点
,点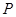 是曲线
是曲线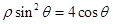 上任一点,设点
上任一点,设点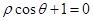 的距离为
的距离为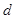 ,则
,则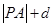 的最小值为 .
的最小值为 .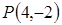 的抛物线的标准方程为( )
的抛物线的标准方程为( )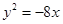
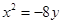
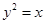 或
或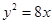
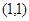 的抛物线的标准方程是 .
的抛物线的标准方程是 .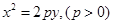 焦点为
焦点为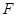 ,过
,过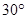 的直线,与抛物线交于A,B两点,若
的直线,与抛物线交于A,B两点,若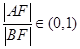 ,则
,则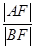 = ( )
= ( )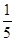
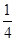

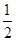
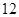 点时,拱顶离水面
点时,拱顶离水面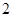 米,桥下的水面宽
米,桥下的水面宽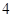 米;下午
米;下午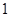 米,桥下的水面宽 米.
米,桥下的水面宽 米.