题目内容
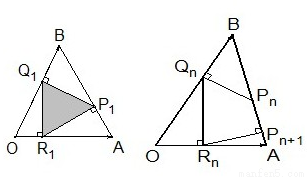
已知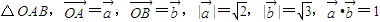 ,边AB上一点P1,这里P1异于A、B.由P1引边OB的垂线P1Q1,Q1是垂足,再由Q1引边OA的垂线Q1R1,R1是垂足.又由R1引边AB的垂线R1P2,P2是垂足.同样的操作连续进行,得到点 Pn、Qn、Rn(n∈N*).设
,边AB上一点P1,这里P1异于A、B.由P1引边OB的垂线P1Q1,Q1是垂足,再由Q1引边OA的垂线Q1R1,R1是垂足.又由R1引边AB的垂线R1P2,P2是垂足.同样的操作连续进行,得到点 Pn、Qn、Rn(n∈N*).设 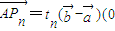 <tn<1),如图.
<tn<1),如图.(1)求
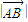 的值;
的值;(2)某同学对上述已知条件的研究发现如下结论:
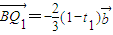 ,问该同学这个结论是否正确?并说明理由;
,问该同学这个结论是否正确?并说明理由;(3)用t1和n表示tn.
【答案】分析:(1)欲求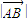 的值,先求其平方.利用三角形OAB中的边角条件即可求得
的值,先求其平方.利用三角形OAB中的边角条件即可求得 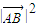 ,从而得出
,从而得出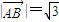 ;
;
(2)该同学的结论正确.由(1)与已知,得三角形OAB的三边长,由余弦定理结合向量条件即可证得.
(3)结合图形,可得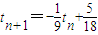 变形为:
变形为: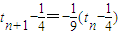 得到{tn-
得到{tn- }构成一个等比数列,公比为-
}构成一个等比数列,公比为- ,利用等比数列的通项公式即可表示出tn
,利用等比数列的通项公式即可表示出tn
解答:解:(1)因为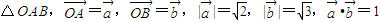 -----(1分)
-----(1分)
则 ;所以,
;所以,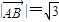 --------------(4分)
--------------(4分)
(2)该同学的结论正确.----------------------------(5分)
由(1)与已知,得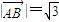 ,
,
由余弦定理 -----------------(6分)
-----------------(6分)
又∵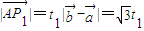 ,则
,则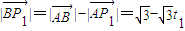
则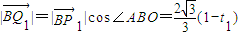 ,所以,
,所以,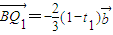 ---------(8分)
---------(8分)
(3)结合图形,可得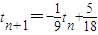 ---------------------(14分)
---------------------(14分)
则 ------------------------(16分)
------------------------(16分)
∴{tn- }构成一个等比数列,公比为-
}构成一个等比数列,公比为- ,
,
故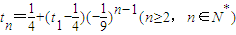 --------------(18分)
--------------(18分)
点评:本小题主要考查向量模、解三角形的应用、数列的通项公式等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
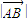 的值,先求其平方.利用三角形OAB中的边角条件即可求得
的值,先求其平方.利用三角形OAB中的边角条件即可求得 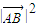 ,从而得出
,从而得出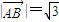 ;
;(2)该同学的结论正确.由(1)与已知,得三角形OAB的三边长,由余弦定理结合向量条件即可证得.
(3)结合图形,可得
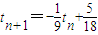 变形为:
变形为: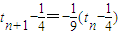 得到{tn-
得到{tn- }构成一个等比数列,公比为-
}构成一个等比数列,公比为- ,利用等比数列的通项公式即可表示出tn
,利用等比数列的通项公式即可表示出tn解答:解:(1)因为
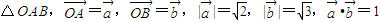 -----(1分)
-----(1分)则
 ;所以,
;所以,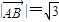 --------------(4分)
--------------(4分)(2)该同学的结论正确.----------------------------(5分)
由(1)与已知,得
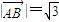 ,
,
由余弦定理
 -----------------(6分)
-----------------(6分)又∵
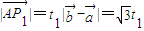 ,则
,则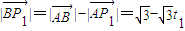
则
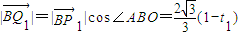 ,所以,
,所以,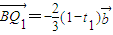 ---------(8分)
---------(8分)(3)结合图形,可得
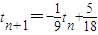 ---------------------(14分)
---------------------(14分)则
 ------------------------(16分)
------------------------(16分)∴{tn-
 }构成一个等比数列,公比为-
}构成一个等比数列,公比为- ,
,故
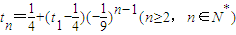 --------------(18分)
--------------(18分)点评:本小题主要考查向量模、解三角形的应用、数列的通项公式等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
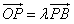 ,点Q是边AB上一点,且
,点Q是边AB上一点,且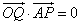 。
。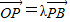 ,点Q是边AB上一点,且
,点Q是边AB上一点,且 .
.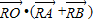 的取值范围.
的取值范围.