题目内容
已知△ABC,且AC=BC,若P0是边AB上一定点,若对于边AB上任一点P,恒有
•
≥
•
则 ( )
| PB |
| PC |
| P0B |
| P0C |
分析:以AB所在的直线为x轴,以AB的中垂线为y轴建立直角坐标系,设AB=4,C(0,b),P(x,0),x∈[-2,2],P0(m,0),然后根据对于边AB上任一点P,恒有
•
≥
•
建立关系式,转化成坐标关系,从而可求出所求.
| PB |
| PC |
| P0B |
| P0C |
解答:解: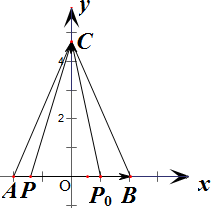 以AB所在的直线为x轴,以AB的中垂线为y轴建立直角坐标系,
以AB所在的直线为x轴,以AB的中垂线为y轴建立直角坐标系,
∵△ABC,且AC=BC,
∴设AB=4,C(0,b),P(x,0),x∈[-2,2],P0(m,0),
则A(-2,0),B(2,0),
∴
=(2-x,0),
=(-x,b),
=(2-m,0),
=(-m,b),
∵对于边AB上任一点P,恒有
•
≥
•
,
∴(2-x)(-x)≥(2-m)(-m)在x∈[-2,2]上恒成立,
即m2-2m≤x2-2x在x∈[-2,2]上恒成立,
而函数y=x2-2x在x∈[-2,2]上的最小值为-1,
则m2-2m≤-1,即(m-1)2≤0,
∴m=1,即
=
.
故选D.
 以AB所在的直线为x轴,以AB的中垂线为y轴建立直角坐标系,
以AB所在的直线为x轴,以AB的中垂线为y轴建立直角坐标系,∵△ABC,且AC=BC,
∴设AB=4,C(0,b),P(x,0),x∈[-2,2],P0(m,0),
则A(-2,0),B(2,0),
∴
| PB |
| PC |
| P0B |
| P0C |
∵对于边AB上任一点P,恒有
| PB |
| PC |
| P0B |
| P0C |
∴(2-x)(-x)≥(2-m)(-m)在x∈[-2,2]上恒成立,
即m2-2m≤x2-2x在x∈[-2,2]上恒成立,
而函数y=x2-2x在x∈[-2,2]上的最小值为-1,
则m2-2m≤-1,即(m-1)2≤0,
∴m=1,即
| P0B |
| 1 |
| 4 |
| AB |
故选D.
点评:本题主要考查了平面向量的运算,向量的数量积的概念,向量运算的几何意义的应用,还考查了利用向量解决简单的几何问题的能力和转化的思想.属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目

 (2012•浦东新区一模)世博中学为了落实上海市教委推出的“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地,如图点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x,x∈[10,20].
(2012•浦东新区一模)世博中学为了落实上海市教委推出的“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地,如图点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x,x∈[10,20].