题目内容
已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,-3),点P的横坐标为14,且| OP |
| PB |
| OQ |
| AP |
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标;
(3)若R为线段OQ上的一个动点,试求
| RO |
| RA |
| RB |
分析:(1)先设P(14,y),分别表示
,
然后由
=λ
,建立关于y的方程可求y.
(2)先设点Q(a,b),则可表示向量
,由
•
=0,可得3a=4b,再由点Q在边AB上可得
=
①②,从而可解a,b,进而可得Q的坐标.
(3)由R为线段OQ上的一个动点可设R(4t,3t),且0≤t≤1,则有分别表示
,
+
,由向量的数量积整理可得
•(
+
)=50t2-50t,利用二次函数的知识可求取值范围.
| OP |
| PB |
| OP |
| PB |
(2)先设点Q(a,b),则可表示向量
| OQ |
| OQ |
| AP |
| 12 |
| -4 |
| b+3 |
| a-6 |
(3)由R为线段OQ上的一个动点可设R(4t,3t),且0≤t≤1,则有分别表示
| RO |
| RA |
| RB |
| RO |
| RA |
| RB |
解答:解:(1)设P(14,y),则
=(14,y),
=(-8,-3-y),由
=λ
,得(14,y)=λ(-8,-3-y),解得λ=-
,y=-7,所以点P(14,-7).
(2)设点Q(a,b),则
=(a,b),又
=(12,-16),则由
•
=0,得3a=4b①又点Q在边AB上,所以
=
,即3a+b-15=0②
联立①②,解得a=4,b=3,所以点Q(4,3).
(3)因为R为线段OQ上的一个动点,故设R(4t,3t),且0≤t≤1,则
=(-4t,-3t),
=(2-4t,9-3t),
=(6-4t,-3-3t),
+
=(8-8t,6-6t),则
•(
+
)=-4t(8-8t)-3t(6-6t)=50t2-50t=50(t-
)2-
(0≤t≤1),故
•(
+
)的取值范围为[-
,0].
| OP |
| PB |
| OP |
| PB |
| 7 |
| 4 |
(2)设点Q(a,b),则
| OQ |
| AP |
| OQ |
| AP |
| 12 |
| -4 |
| b+3 |
| a-6 |
联立①②,解得a=4,b=3,所以点Q(4,3).
(3)因为R为线段OQ上的一个动点,故设R(4t,3t),且0≤t≤1,则
| RO |
| RA |
| RB |
| RA |
| RB |
| RO |
| RA |
| RB |
| 1 |
| 2 |
| 25 |
| 2 |
| RO |
| RA |
| RB |
| 25 |
| 2 |
点评:平面向量与函数的综合问题中,向量的数量积、向量的平行一般是作为转化的基本工具,最后转化为函数的问题,二次函数在闭区间上的最值是求解是函数性质应用中容易出现错误的地方.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
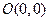 ,
,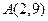 ,
,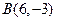 , 点P的横坐标为14,且
, 点P的横坐标为14,且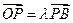 ,点
,点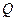 是边
是边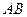 上一点,且
上一点,且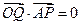 .
.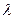 的值与点
的值与点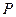 的坐标;
的坐标;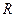 为线段
为线段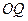 上的一个动点,试求
上的一个动点,试求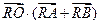 的取值范围.
的取值范围. ,
, ,
, , 点P的横坐标为14,且
, 点P的横坐标为14,且 ,点
,点 是边
是边 上一点,且
上一点,且 .
. 的值与点
的值与点 的坐标;
的坐标; 为线段
为线段 上的一个动点,试求
上的一个动点,试求 的取值范围.
的取值范围.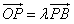 ,点Q是边AB上一点,且
,点Q是边AB上一点,且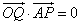 。
。