题目内容
18.若P为△ABC内一点,且满足$\overrightarrow{PA}$+2$\overrightarrow{PB}$+3$\overrightarrow{PC}$=0,则△ABC的面积与△APC的面积之比为1:3.分析 可延长PB到B′,延长PC到C′,并分别使PB′=2PB,PC′=3PC,从而根据条件便得到:$\overrightarrow{PA}+\overrightarrow{PB′}+\overrightarrow{PC′}=\overrightarrow{0}$,这便说明P为△AB′C′的重心.这便得到三角形PAB′,三角形PB′C′,及三角形PC′A的面积都相等,设为S,从而会得到S△ABC=S,${S}_{△APC}=\frac{1}{3}S$,这样便可求出△ABC的面积与△APC的面积之比.
解答 解:如图,延长PB至PB',使PB'=2PB,延长PC至PC',使PC'=3PC,并连接AB′,B′C′,C′A,则:
$\overrightarrow{PA}+2\overrightarrow{PB}+3\overrightarrow{PC}$=$\overrightarrow{PA}+\overrightarrow{PB′}+\overrightarrow{PC′}=\overrightarrow{0}$;
∴P是△AB′C′的重心;
∴△PAB′,△PB′C′,△PC′A三个三角形的面积相等,记为S;
∴${S}_{△APB}=\frac{S}{2},{S}_{△APC}=\frac{S}{3},{S}_{BPC}=\frac{S}{6}$;
∴${S}_{△ABC}=\frac{S}{2}+\frac{S}{3}+\frac{S}{6}=S$;
∴S△APC:S△ABC=1:3.
故答案为:1:3.
点评 考查向量数乘的几何意义,三角形重心和三顶点构成向量的和为零向量,以及三角形的面积公式.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
9.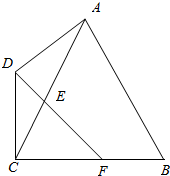 如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )
如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )
 如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )
如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{3}{4}$ | D. | -1 |
8.甲乙两人相约打靶,甲射击3次,每次射击的命中率为$\frac{1}{2}$,乙射击2次,每次射击的命中率为$\frac{2}{3}$,记甲命中的次数为x,乙命中的次数为y
(1)求x+y的分布列和E(x+y)
(2)猜想两个相互独立的变量x,y的期望与x+y的期望间的关系,并证明你的猜想.
其中,x的分布列为:
y的分布列为:
(1)求x+y的分布列和E(x+y)
(2)猜想两个相互独立的变量x,y的期望与x+y的期望间的关系,并证明你的猜想.
其中,x的分布列为:
| x | x1 | x2 | … | xn |
| p | p1 | p2 | pn |
| y | y1 | y2 | … | ym |
| p | p${\;}_{1}^{′}$ | p${\;}_{2}^{′}$ | … | p${\;}_{m}^{′}$ |
 在△ABC中,P为AB的中点,O在边AC上,且|$\overrightarrow{AO}$|=2|$\overrightarrow{OC}$|,BO∩CP=R,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.
在△ABC中,P为AB的中点,O在边AC上,且|$\overrightarrow{AO}$|=2|$\overrightarrow{OC}$|,BO∩CP=R,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.