题目内容
(2011•普宁市模拟)已知:
=(1,sinx-1),
=(sinx+sinxcosx,sinx),f(x)=
•
.(x∈R)
求:(1)函数f(x)的最大值和最小正周期;
(2)函数f(x)的单调递增区间.
| OA |
| OB |
| OA |
| OB |
求:(1)函数f(x)的最大值和最小正周期;
(2)函数f(x)的单调递增区间.
分析:(1)先把
,
的坐标代入 f(x)=
•
,化简,即可得到求函数f(x)的解析式,再根据三角函数的二倍角公式和两角和与差的正弦公式将函数化简为y=Asin(wx+ρ)的形式,最后利用三角函数的性质即可得到答案.
(2)由(1)得出f(x)的表达式,根据将2x-
看做一个整体,令 2kπ-
≤2x-
≤2kπ+
,k∈Z解出x的范围即可得到答案.
| OA |
| OB |
| OA |
| OB |
(2)由(1)得出f(x)的表达式,根据将2x-
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
解答:解:(1)f(x)=
•
=sinx+sinxcosx+sin2x-sinx…(2分)
=
sin(2x-
)+
…(4分)∴x=kπ+
(k∈Z)时,
f(x)取得最大值
,…(6分)
最小正周期为π.…(8分)
(2)当2kπ-
≤2x-
≤2kπ+
,k∈Z…(10分)
即kπ-
≤x≤kπ+
,k∈Z时函数为增函数 …(11分)
∴原函数的递增区间是[kπ-
,kπ+
](k∈Z).…(12分)
| OA |
| OB |
=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 3π |
| 8 |
f(x)取得最大值
1+
| ||
| 2 |
最小正周期为π.…(8分)
(2)当2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
即kπ-
| π |
| 8 |
| 3π |
| 8 |
∴原函数的递增区间是[kπ-
| π |
| 8 |
| 3π |
| 8 |
点评:本题借助向量的坐标运算,考查三角函数的单调区间和值域的问题.一般先将函数化简为y=Asin(wx+ρ)的形式,再根据正弦函数的图象和性质解题.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
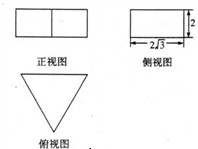 (2011•普宁市模拟)若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )
(2011•普宁市模拟)若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )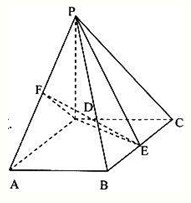 (2011•普宁市模拟)如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AD=2,∠BAD=60°,E、F分别为BC、PA的中点.
(2011•普宁市模拟)如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AD=2,∠BAD=60°,E、F分别为BC、PA的中点.