题目内容
(2011•普宁市模拟)已知数列{am}是首项为a,公差为b的等差数列,{bn}是首项为b,公比为a的等比数列,且满足a1<b1<a2<b2<a3,其中a、b、m、n∈N*.
(Ⅰ)求a的值;
(Ⅱ)若数列{1+am}与数列{bn}有公共项,将所有公共项按原顺序排列后构成一个新数列{cn},求数列{cn}的通项公式;
(Ⅲ)记(Ⅱ)中数列{cn}的前项之和为Sn,求证:
+
+
+…+
<
(n≥3).
(Ⅰ)求a的值;
(Ⅱ)若数列{1+am}与数列{bn}有公共项,将所有公共项按原顺序排列后构成一个新数列{cn},求数列{cn}的通项公式;
(Ⅲ)记(Ⅱ)中数列{cn}的前项之和为Sn,求证:
| 9 |
| S1S2 |
| 9 |
| S2S3 |
| 9 |
| S3S4 |
| 9 |
| SnSn+1 |
| 19 |
| 42 |
分析:(Ⅰ)由题设am=a+(m-1)b,知bn=b•an-1.由a<b<a+b<ab<a+2b,知ab<a+2b<3b.由此能求出a.
(Ⅱ)设1+a+(m-1)b=b•an-1.由a=2,知3+(m-1)b=b•2n-1,所以b=
.由此能求出cn.
(Ⅲ)由Sn=3(1+2+…+2n-1)=3(2n-1).知当n≥3时,2n-1=Cn0+Cn1+…+Cnn-1+Cnn-1≥Cn0+Cn1+Cnn-1+Cnn-1=2n+1,当且仅当n=3时等号成立,所以Sn≥3(2n+1).由此能够证明
+
+
+…+
<
(n≥3).
(Ⅱ)设1+a+(m-1)b=b•an-1.由a=2,知3+(m-1)b=b•2n-1,所以b=
| 3 |
| 2n-1-(m-1) |
(Ⅲ)由Sn=3(1+2+…+2n-1)=3(2n-1).知当n≥3时,2n-1=Cn0+Cn1+…+Cnn-1+Cnn-1≥Cn0+Cn1+Cnn-1+Cnn-1=2n+1,当且仅当n=3时等号成立,所以Sn≥3(2n+1).由此能够证明
| 9 |
| S1S2 |
| 9 |
| S2S3 |
| 9 |
| S3S4 |
| 9 |
| SnSn+1 |
| 19 |
| 42 |
解答:解:(Ⅰ)由题设am=a+(m-1)b,bn=b•an-1. …(1分)
由已知a<b<a+b<ab<a+2b,所以ab<a+2b<3b.
又b>0,所以a<3. …(2分)
因为ab>a+b,b>a,则ab>2a.又a>0,
所以b>2,从而有a>
>1. …(3分)
因为a∈N*,故a=2. …(4分)
(Ⅱ)设1+am=bn,即1+a+(m-1)b=b•an-1. …(5分)
因为a=2,则3+(m-1)b=b•2n-1,
所以b=
. …(6分)
因为b>a=2,且b∈N*,所以2n-1-(m-1)=1,
即m=2n-1,且b=3. …(7分)
故cn=bn=3•2n-1. …(8分)
(Ⅲ)由题设,Sn=3(1+2+…+2n-1)=3(2n-1). …(9分)
当n≥3时,2n-1=Cn0+Cn1+…+Cnn-1+Cnn-1≥Cn0+Cn1+Cnn-1+Cnn-1=2n+1,当且仅当n=3时等号成立,
所以Sn≥3(2n+1). …(11分)
于是
=
<
=
[
-
](n≥3).
(12分)
因为S1=3,S2=9,S3=21,则
+
+
+…+
<
+
+
[
-
+
-
+…
-
]
=
+
+
(
-
)<
+
+
=
. …(14分)
由已知a<b<a+b<ab<a+2b,所以ab<a+2b<3b.
又b>0,所以a<3. …(2分)
因为ab>a+b,b>a,则ab>2a.又a>0,
所以b>2,从而有a>
| b |
| b-1 |
因为a∈N*,故a=2. …(4分)
(Ⅱ)设1+am=bn,即1+a+(m-1)b=b•an-1. …(5分)
因为a=2,则3+(m-1)b=b•2n-1,
所以b=
| 3 |
| 2n-1-(m-1) |
因为b>a=2,且b∈N*,所以2n-1-(m-1)=1,
即m=2n-1,且b=3. …(7分)
故cn=bn=3•2n-1. …(8分)
(Ⅲ)由题设,Sn=3(1+2+…+2n-1)=3(2n-1). …(9分)
当n≥3时,2n-1=Cn0+Cn1+…+Cnn-1+Cnn-1≥Cn0+Cn1+Cnn-1+Cnn-1=2n+1,当且仅当n=3时等号成立,
所以Sn≥3(2n+1). …(11分)
于是
| 9 |
| Snsn+1 |
| 1 |
| (2n-1)(2n+1-1) |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
(12分)
因为S1=3,S2=9,S3=21,则
| 9 |
| S1S2 |
| 9 |
| S2S3 |
| 9 |
| S3S4 |
| 9 |
| SnSn+1 |
| 1 |
| 3 |
| 1 |
| 21 |
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 9 |
| 1 |
| 11 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
=
| 1 |
| 3 |
| 1 |
| 21 |
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 2n+3 |
| 1 |
| 3 |
| 1 |
| 21 |
| 1 |
| 14 |
| 19 |
| 42 |
点评:本题考查数列的综合运用,解题时要认真审题,仔细解答,合理地运用放缩法进行证明.注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
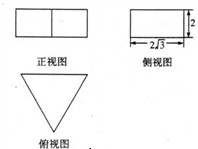 (2011•普宁市模拟)若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )
(2011•普宁市模拟)若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )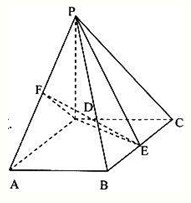 (2011•普宁市模拟)如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AD=2,∠BAD=60°,E、F分别为BC、PA的中点.
(2011•普宁市模拟)如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AD=2,∠BAD=60°,E、F分别为BC、PA的中点.