题目内容
(2011•普宁市模拟)下列命题中,正确的是( )
分析:A:命题:任意的x∈R,x2-x≤0的否定是只否定结论
B:先写出命题若aπ2≤bπ2则a≤b的否命题,然后判断真假
C:若P且q为真,则p,q都为真,此时p或q为真;若p或q 为真,则p,q至少一个为真,p且q不一定为真,从而可判断
D:若实x,y∈[-1,1],则x,y所表示的区域是边长为2的正方形,面积为4,x2+y2≥1表示的区域是正方形内的圆及圆外的区域,面积为4-π,由几何概率的公式可求概率
B:先写出命题若aπ2≤bπ2则a≤b的否命题,然后判断真假
C:若P且q为真,则p,q都为真,此时p或q为真;若p或q 为真,则p,q至少一个为真,p且q不一定为真,从而可判断
D:若实x,y∈[-1,1],则x,y所表示的区域是边长为2的正方形,面积为4,x2+y2≥1表示的区域是正方形内的圆及圆外的区域,面积为4-π,由几何概率的公式可求概率
解答:解:A:命题:任意的x∈R,x2-x≤0的否定是:任意的x∈R,x2-x≤0,A错误
B:若aπ2≤bπ2则a≤b的否命题为:若a>b,则aπ2>bπ2,此命题为真,故B正确
C:若P且q为真,则p,q都为真,此时p或q为真;若p或q 为真,则p,q至少一个为真,p且q不一定为真,即p且q为真是p或q为着的充分不必要条件,故C错误
D:若实x,y∈[-1,1],则x,y所表示的区域是边长为2的正方形,面积为4,x2+y2≥1表示的区域是正方形内的圆及圆外的区域,面积为4-π,由几何概率的公式可得P=1-
,故D错误
故选:B
B:若aπ2≤bπ2则a≤b的否命题为:若a>b,则aπ2>bπ2,此命题为真,故B正确
C:若P且q为真,则p,q都为真,此时p或q为真;若p或q 为真,则p,q至少一个为真,p且q不一定为真,即p且q为真是p或q为着的充分不必要条件,故C错误
D:若实x,y∈[-1,1],则x,y所表示的区域是边长为2的正方形,面积为4,x2+y2≥1表示的区域是正方形内的圆及圆外的区域,面积为4-π,由几何概率的公式可得P=1-
| π |
| 4 |
故选:B
点评:本题主要考查了命题的真假判断,解题的关键是熟练应用命题的否定及否命题的写法及真假判断,复合命题的真假判断,与面积有关的几何概率的求解.

练习册系列答案
相关题目
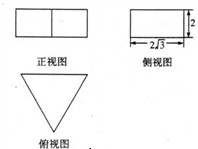 (2011•普宁市模拟)若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )
(2011•普宁市模拟)若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )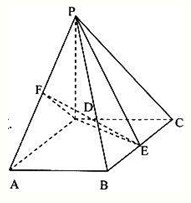 (2011•普宁市模拟)如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AD=2,∠BAD=60°,E、F分别为BC、PA的中点.
(2011•普宁市模拟)如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AD=2,∠BAD=60°,E、F分别为BC、PA的中点.