题目内容
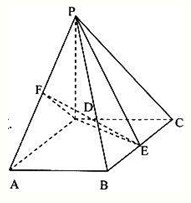 (2011•普宁市模拟)如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AD=2,∠BAD=60°,E、F分别为BC、PA的中点.
(2011•普宁市模拟)如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AD=2,∠BAD=60°,E、F分别为BC、PA的中点.(I)求证:ED⊥平面PAD;
(Ⅱ)求三棱锥P-DEF的体积;
(Ⅲ)求平面PAD与平面PBC所成的锐二面角大小的余弦值.
分析:(I) 要证DE⊥平面PAD. 关键是证明DE⊥AD,PD⊥DE,利用条件线面垂直可证;
(Ⅱ)利用转化底面的方法可求三棱锥P-DEF的体积,即VP-DEF=VE-PDF;
(Ⅲ) 建立空间直角坐标系,利用平面的法向量的夹角求平面PAD与平面PBC所成的锐二面角大小的余弦值.
(Ⅱ)利用转化底面的方法可求三棱锥P-DEF的体积,即VP-DEF=VE-PDF;
(Ⅲ) 建立空间直角坐标系,利用平面的法向量的夹角求平面PAD与平面PBC所成的锐二面角大小的余弦值.
解答:证明:(I)连接BD,由已知得BD=2,

在正三角形BCD中,BE=EC,∴DE⊥BC,又AD∥BC,∴DE⊥AD…(2分)
又PD⊥平面ABCD,∴PD⊥DE,…(3分)
AD∩PD=D,∴DE⊥平面PAD. …(4分)
(Ⅱ)∵S△PDF=
•S△PDA=
×
×22=1,
且DE=
,…(5分)
∴VP-DEF=VE-PDF=
•S△PDF•DE=
×1×
=
…(8分)
(Ⅲ):如图建立空间直角坐标系D-AEP,
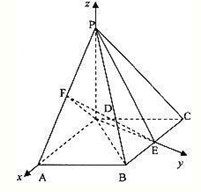
则由(I)知平面PAD的一个法向量为
=(0,1,0)∵B(1,
,0),C(-1,
,0),P(0,0,2),∴
=(2,0,0),
=(1,
,-2)
设平面PBC的法向量为
=(x,y,z),
由
,∴
取y=2得
=(0,2,
)…(11分)∴cos?
,
>=
=
=
…(13分)
∴平面PAD与平面PBC所成的锐二面角大小的余弦值为
…(14分)

在正三角形BCD中,BE=EC,∴DE⊥BC,又AD∥BC,∴DE⊥AD…(2分)
又PD⊥平面ABCD,∴PD⊥DE,…(3分)
AD∩PD=D,∴DE⊥平面PAD. …(4分)
(Ⅱ)∵S△PDF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
且DE=
| 3 |
∴VP-DEF=VE-PDF=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| ||
| 3 |
(Ⅲ):如图建立空间直角坐标系D-AEP,

则由(I)知平面PAD的一个法向量为
| n1 |
| 3 |
| 3 |
| CB |
| PB |
| 3 |
设平面PBC的法向量为
| n2 |
由
|
|
取y=2得
| n2 |
| 3 |
| n1 |
| n2 |
| ||||
|
|
| 2 | ||
1•
|
2
| ||
| 7 |
∴平面PAD与平面PBC所成的锐二面角大小的余弦值为
2
| ||
| 7 |
点评:本题的考点是用空间向量其余平面的夹角,主要考查线面垂直,考查面面角,关键是建立坐标系,求平面的法向量.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
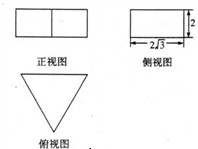 (2011•普宁市模拟)若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )
(2011•普宁市模拟)若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )